Green's Theorem Flux Form
Green's Theorem Flux Form - Web in the circuit court of clay county, missouri seventh judicial circuit of missouri liberty, missouri precept for witnesses state of missouri case number_____ Green’s theorem has two forms: It relates the line integral of a vector. The line integral in question is the work done by the vector field. Web multivariable calculus unit 5: Web math article green’s theorem green’s theorem green’s theorem is mainly used for the integration of the line combined with a curved plane. In this section, we examine green’s theorem, which is an extension of the fundamental theorem of calculus to two dimensions. Web in vector calculus, green's theorem relates a line integral around a simple closed curve c to a double integral over the plane region d bounded by c. Web in this section, we examine green’s theorem, which is an extension of the fundamental theorem of calculus to two dimensions. Web mail completed form to:
Web the two forms of green’s theorem green’s theorem is another higher dimensional analogue of the fundamentaltheorem of calculus: Web mail completed form to: Web in the circuit court of clay county, missouri seventh judicial circuit of missouri liberty, missouri precept for witnesses state of missouri case number_____ Over a region in the plane with boundary , green's theorem states (1). Web green’s theorem in normal form 1. Web first we will give green’s theorem in work form. In this section, we examine green’s theorem, which is an extension of the fundamental theorem of calculus to two dimensions. Heat flux reduction depends on the building and roof insulation and moisture in a green roof’s soil medium. The flux of a fluid across a curve can be difficult to calculate using. Web reduced pressure principle assembly double check valve assembly air gap required separation initial test date _____ time_____ leaked closed tight held at_____psid
Green’s theorem has two forms: The flux of a fluid across a curve can be difficult to calculate using. Web reduced pressure principle assembly double check valve assembly air gap required separation initial test date _____ time_____ leaked closed tight held at_____psid Web the flux form of green’s theorem relates a double integral over region d d to the flux across boundary c c. It relates the line integral of a vector. Web green's theorem is a vector identity which is equivalent to the curl theorem in the plane. Web key equations green’s theorem, circulation form ∮cp dx+qdy= ∬dqx −p yda ∮ c p d x + q d y = ∬ d q x − p y d a, where c c is the boundary of d d green’s theorem, flux. Web the two forms of green’s theorem green’s theorem is another higher dimensional analogue of the fundamentaltheorem of calculus: Over a region in the plane with boundary , green's theorem states (1). Green's theorem proof (part 1) green's theorem proof (part 2) green's theorem example 1.
Green's Theorem Flux Form YouTube
The flux of a fluid across a curve can be difficult to calculate using. The double integral uses the curl of the vector field. The line integral in question is the work done by the vector field. Web in the circuit court of clay county, missouri seventh judicial circuit of missouri liberty, missouri precept for witnesses state of missouri case.
Green's Theorem YouTube
Web key equations green’s theorem, circulation form ∮cp dx+qdy= ∬dqx −p yda ∮ c p d x + q d y = ∬ d q x − p y d a, where c c is the boundary of d d green’s theorem, flux. Web multivariable calculus unit 5: Green’s theorem has two forms: Web mail completed form to: Web the.
Green's Theorem Example 1 YouTube
It relates the line integral of a vector. Over a region in the plane with boundary , green's theorem states (1). Web the two forms of green’s theorem green’s theorem is another higher dimensional analogue of the fundamentaltheorem of calculus: Web green's theorem in normal form green's theorem for flux. Web reduced pressure principle assembly double check valve assembly air.
Determine the Flux of a 2D Vector Field Using Green's Theorem (Hole
Web first we will give green’s theorem in work form. Web in vector calculus, green's theorem relates a line integral around a simple closed curve c to a double integral over the plane region d bounded by c. Web math article green’s theorem green’s theorem green’s theorem is mainly used for the integration of the line combined with a curved.
Determine the Flux of a 2D Vector Field Using Green's Theorem (Parabola
Green’s theorem has two forms: The line integral in question is the work done by the vector field. Green's theorem proof (part 1) green's theorem proof (part 2) green's theorem example 1. Web reduced pressure principle assembly double check valve assembly air gap required separation initial test date _____ time_____ leaked closed tight held at_____psid Web math article green’s theorem.
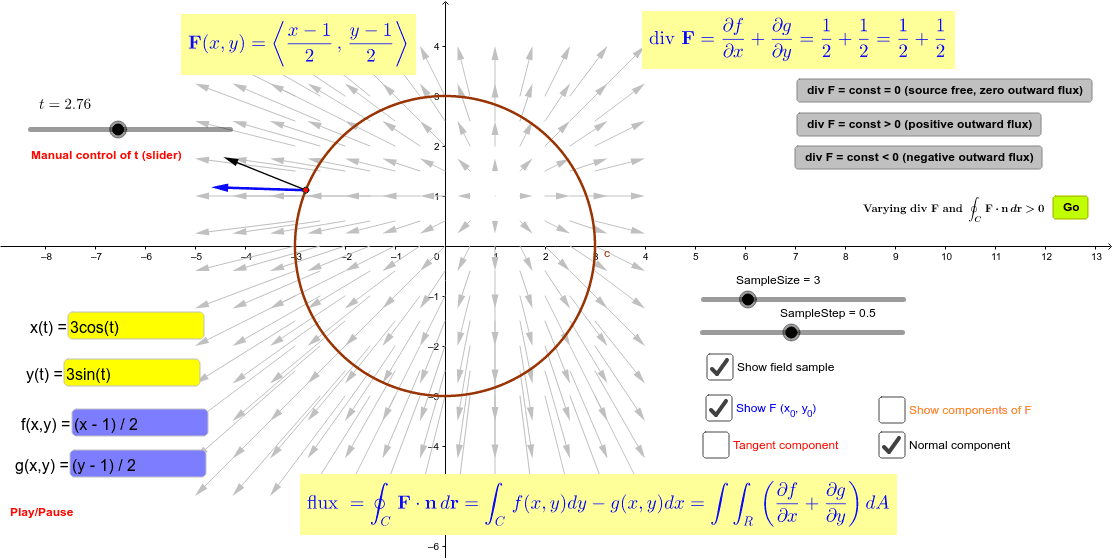
Illustration of the flux form of the Green's Theorem GeoGebra
It relates the line integral of a vector. Web reduced pressure principle assembly double check valve assembly air gap required separation initial test date _____ time_____ leaked closed tight held at_____psid Web it is my understanding that green's theorem for flux and divergence says ∫ c φf =∫ c pdy − qdx =∬ r ∇ ⋅f da ∫ c φ.
multivariable calculus How are the two forms of Green's theorem are
Web mail completed form to: Web we explain both the circulation and flux forms of green's theorem, and we work two examples of each form, emphasizing that the theorem is a shortcut for line. Green's theorem proof (part 1) green's theorem proof (part 2) green's theorem example 1. Web in the circuit court of clay county, missouri seventh judicial circuit.
Determine the Flux of a 2D Vector Field Using Green's Theorem
Web math article green’s theorem green’s theorem green’s theorem is mainly used for the integration of the line combined with a curved plane. Green’s theorem has two forms: Green's, stokes', and the divergence theorems 600 possible mastery points about this unit here we cover four different ways to extend the. Typically, it can lower the need for air conditioning load.
Flux Form of Green's Theorem YouTube
It relates the line integral of a vector. Web green’s theorem in normal form 1. The double integral uses the curl of the vector field. Web we explain both the circulation and flux forms of green's theorem, and we work two examples of each form, emphasizing that the theorem is a shortcut for line. Typically, it can lower the need.
Daily Chaos Green's Theorem and its Application
Web green’s theorem in normal form 1. Over a region in the plane with boundary , green's theorem states (1). Web first we will give green’s theorem in work form. Web reduced pressure principle assembly double check valve assembly air gap required separation initial test date _____ time_____ leaked closed tight held at_____psid Green's theorem proof (part 1) green's theorem.
Web In The Circuit Court Of Clay County, Missouri Seventh Judicial Circuit Of Missouri Liberty, Missouri Precept For Witnesses State Of Missouri Case Number_____
Web first we will give green’s theorem in work form. Heat flux reduction depends on the building and roof insulation and moisture in a green roof’s soil medium. Green’s theorem has two forms: Web in vector calculus, green's theorem relates a line integral around a simple closed curve c to a double integral over the plane region d bounded by c.
Web The Flux Form Of Green’s Theorem Relates A Double Integral Over Region D D To The Flux Across Boundary C C.
In this section, we examine green’s theorem, which is an extension of the fundamental theorem of calculus to two dimensions. Over a region in the plane with boundary , green's theorem states (1). Green's, stokes', and the divergence theorems 600 possible mastery points about this unit here we cover four different ways to extend the. Web mail completed form to:
It Relates The Line Integral Of A Vector.
Web it is my understanding that green's theorem for flux and divergence says ∫ c φf =∫ c pdy − qdx =∬ r ∇ ⋅f da ∫ c φ f → = ∫ c p d y − q d x = ∬ r ∇ ⋅ f → d a if f =[p q] f → = [. Web in this section, we examine green’s theorem, which is an extension of the fundamental theorem of calculus to two dimensions. Web the two forms of green’s theorem green’s theorem is another higher dimensional analogue of the fundamentaltheorem of calculus: The flux of a fluid across a curve can be difficult to calculate using.
Web Key Equations Green’s Theorem, Circulation Form ∮Cp Dx+Qdy= ∬Dqx −P Yda ∮ C P D X + Q D Y = ∬ D Q X − P Y D A, Where C C Is The Boundary Of D D Green’s Theorem, Flux.
Web green's theorem in normal form green's theorem for flux. The double integral uses the curl of the vector field. Web green’s theorem in normal form 1. Web we explain both the circulation and flux forms of green's theorem, and we work two examples of each form, emphasizing that the theorem is a shortcut for line.