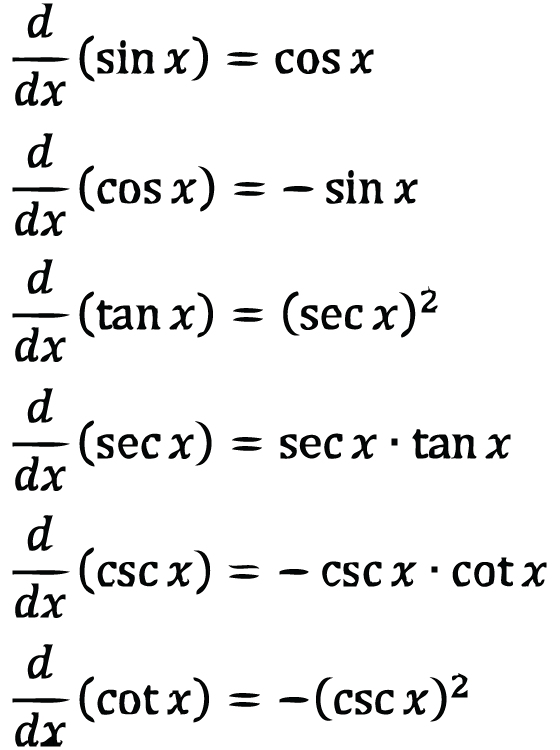Derivative Of Trig Functions Cheat Sheet

Derivative Of Trig Functions Cheat Sheet - D (tan(x)) = sec2(x) dx · x0. Sum difference rule \left (f\pm g\right)^'=f^'\pm g^'. D (cos(x)) = sin(x) dx · x0. D dx (xn) = nxn 1 3. D (cot(x)) = csc2(x) dx · x0. F g 0 = f0g 0fg g2 5. D (sin(x)) = cos(x) · x0 dx. Web trigonometry cheat sheet algebra trigonometry limits derivatives integrals basic identities \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos. D (csc(x)) = csc(x) cot(x) dx · x0. Where c is a constant 2.

Web trigonometry cheat sheet algebra trigonometry limits derivatives integrals basic identities \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos. F g 0 = f0g 0fg g2 5. D (sec(x)) = sec(x) tan(x) · x0 dx. D dx (c) = 0; D (tan(x)) = sec2(x) dx · x0. D (cot(x)) = csc2(x) dx · x0. (fg)0 = f0g +fg0 4. D dx (xn) = nxn 1 3. D (sin(x)) = cos(x) · x0 dx. Where c is a constant 2.

D (csc(x)) = csc(x) cot(x) dx · x0. D (cos(x)) = sin(x) dx · x0. Web derivatives cheat sheet derivative rules 1. D dx (c) = 0; D (tan(x)) = sec2(x) dx · x0. Sum difference rule \left (f\pm g\right)^'=f^'\pm g^'. D (sin(x)) = cos(x) · x0 dx. Web trigonometry cheat sheet algebra trigonometry limits derivatives integrals basic identities \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos. Where c is a constant 2. D (cot(x)) = csc2(x) dx · x0.

Derivatives Cheat Sheet Derivative Trigonometric Functions

D (csc(x)) = csc(x) cot(x) dx · x0. F g 0 = f0g 0fg g2 5. Web derivatives cheat sheet derivative rules 1. D (cos(x)) = sin(x) dx · x0. D (sin(x)) = cos(x) · x0 dx.

Hyperbolic Functions Cheat Sheet

D dx (c) = 0; D (sin(x)) = cos(x) · x0 dx. D (csc(x)) = csc(x) cot(x) dx · x0. D (cot(x)) = csc2(x) dx · x0. Web derivatives cheat sheet derivative rules 1.

Trig derivative identities cheat sheet teevsa

D (cos(x)) = sin(x) dx · x0. D (cot(x)) = csc2(x) dx · x0. D dx (xn) = nxn 1 3. (fg)0 = f0g +fg0 4. Sum difference rule \left (f\pm g\right)^'=f^'\pm g^'.

9 Best Images of Calculus Worksheets Derivatives Inverse Trig

D dx (xn) = nxn 1 3. D (sec(x)) = sec(x) tan(x) · x0 dx. F g 0 = f0g 0fg g2 5. Where c is a constant 2. D dx (c) = 0;

Trigonometric functions and Differentiation Formulas

Web trigonometry cheat sheet algebra trigonometry limits derivatives integrals basic identities \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos. D (cos(x)) = sin(x) dx · x0. D (sin(x)) = cos(x) · x0 dx. Web derivatives cheat sheet derivative rules 1. Sum.

Trig_Cheat_Sheet.pdf Sine Trigonometric Functions

Sum difference rule \left (f\pm g\right)^'=f^'\pm g^'. D dx (c) = 0; (fg)0 = f0g +fg0 4. Where c is a constant 2. D (cot(x)) = csc2(x) dx · x0.

What are Basic Trig Identities or Trigonometric Identities?

D (sec(x)) = sec(x) tan(x) · x0 dx. D dx (xn) = nxn 1 3. (fg)0 = f0g +fg0 4. D dx (c) = 0; D (csc(x)) = csc(x) cot(x) dx · x0.

Worksheets for Trigonometric Derivatives Examples

D dx (xn) = nxn 1 3. F g 0 = f0g 0fg g2 5. D (csc(x)) = csc(x) cot(x) dx · x0. Where c is a constant 2. D (sin(x)) = cos(x) · x0 dx.

Pin by Mihir on MathWorks Basic math skills, Math formulas, Basic math

D (sec(x)) = sec(x) tan(x) · x0 dx. F g 0 = f0g 0fg g2 5. D (cot(x)) = csc2(x) dx · x0. Sum difference rule \left (f\pm g\right)^'=f^'\pm g^'. D dx (c) = 0;

Derivative Rules Cheat Sheet Calculus Ace Tutors Blog

D (tan(x)) = sec2(x) dx · x0. F g 0 = f0g 0fg g2 5. Web derivatives cheat sheet derivative rules 1. D dx (c) = 0; D dx (xn) = nxn 1 3.

Where C Is A Constant 2.

D (sec(x)) = sec(x) tan(x) · x0 dx. D (sin(x)) = cos(x) · x0 dx. D (cos(x)) = sin(x) dx · x0. F g 0 = f0g 0fg g2 5.

Web Derivatives Cheat Sheet Derivative Rules 1.

Web trigonometry cheat sheet algebra trigonometry limits derivatives integrals basic identities \tan (x) = \frac {\sin (x)} {\cos (x)} \tan (x) = \frac {1} {\cot (x)} \cot (x) = \frac {1} {\tan (x)} \cot (x) = \frac {\cos. D (csc(x)) = csc(x) cot(x) dx · x0. Sum difference rule \left (f\pm g\right)^'=f^'\pm g^'. D (cot(x)) = csc2(x) dx · x0.