How To Draw A Centroid Of A Triangle

How To Draw A Centroid Of A Triangle - In this article, we discussed the centroid of a triangle, its formula, derivations, the difference between orthocenter and centroid, and some facts and examples related to the centroid of a triangle. Learn how to construct the centroid of a triangle by using a compass to construct the medians of the triangle. It works by constructing two medians, which intersect at the centroid. Web each of these shapes will have a centroid (\(c\)) or center of mass (\(g\)) listed on the diagram. Given below is a triangle δabc, where three medians ae, bf, and cd meet at g to from the centriod of the triangle. Web if the ratio of corresponding sides of two similar triangles is 4: Centroid of a right triangle using integration formulas. In other words, the centroid will always be 2/3 of the way along. Those lines are the medians. In every triangle, the centroid is always inside the triangle!

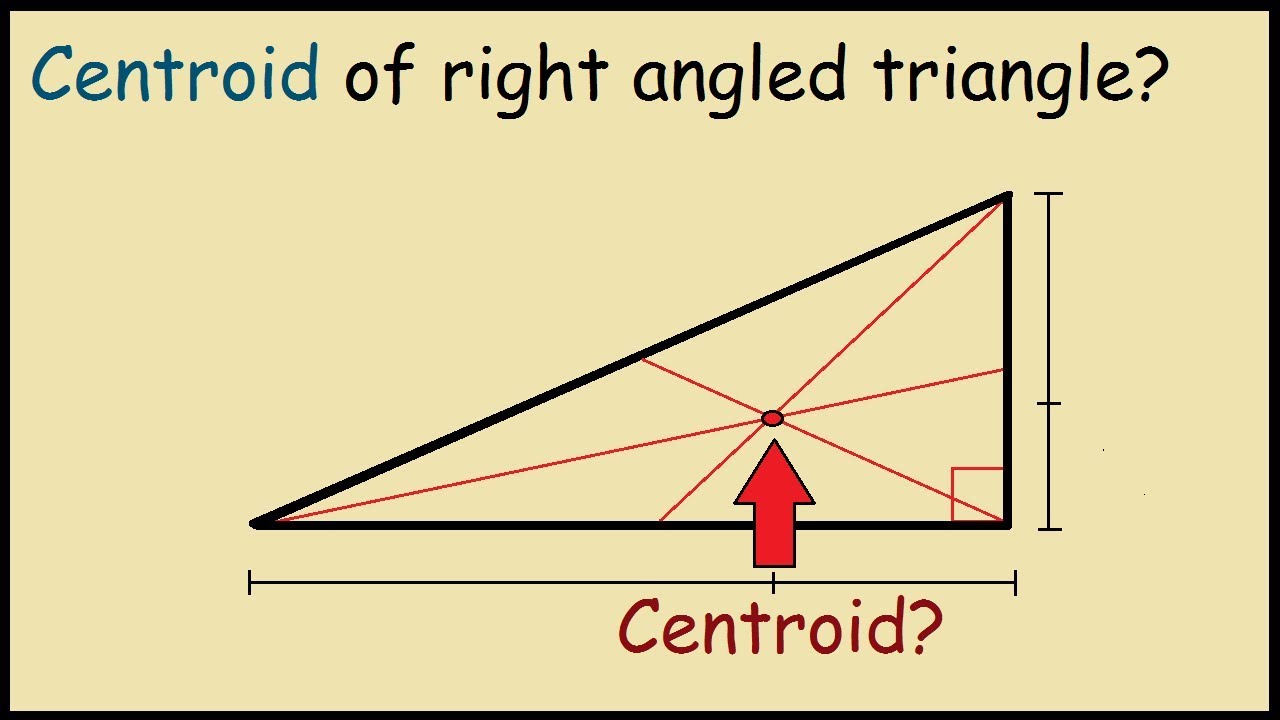
It is referred to as the center of mass or balance point of the triangle. Derive the formulas for the centroid location of the following right triangle. Web there are a few different ways to find the centroid of a triangle. In this article, we discussed the centroid of a triangle, its formula, derivations, the difference between orthocenter and centroid, and some facts and examples related to the centroid of a triangle. It is also the center of gravity of the triangle. We select a coordinate system of x,y axes, with origin at the right angle corner of the triangle and oriented so that they coincide with the two adjacent sides, as depicted in the figure. Web this video shows how to construct the centroid of a triangle by constructing medians. The centroid of a triangle is the point at which the three medians intersect. Web the centroid is positioned inside a triangle; Web the centroid of a triangle is formed when three medians of a triangle intersect.

Set the compass to a length greater than half the length of ab. Web the centroid is the point where the three medi. One way is to draw lines from each vertex (corner) of the triangle to the midpoint of the opposite side. Learn how to construct the centroid of a triangle by using a compass to construct the medians of the triangle. This video tutorial will show you the steps and the commands to use in geogebra. The lines will intersect at the centroid. Web how to construct (draw) the centroid of a triangle with compass and straightedge or ruler. The centroid of a triangle is the point where its medians intersect. 9, then the ratio of areas of these triangles is To find the centroid, we find the midpoint of two sides in the.

Centroid of a right angle triangle (Graphical Proof) YouTube

It is referred to as the center of mass or balance point of the triangle. Then the orthocenter is also outside the triangle. Web how to construct (draw) the centroid of a triangle with compass and straightedge or ruler. Hence, to construct the centroid in a given triangle: Draw an isosceles triangle abc with two sides of the triangle equal.

Centroid of a Triangle Formula, Properties and Example Questions

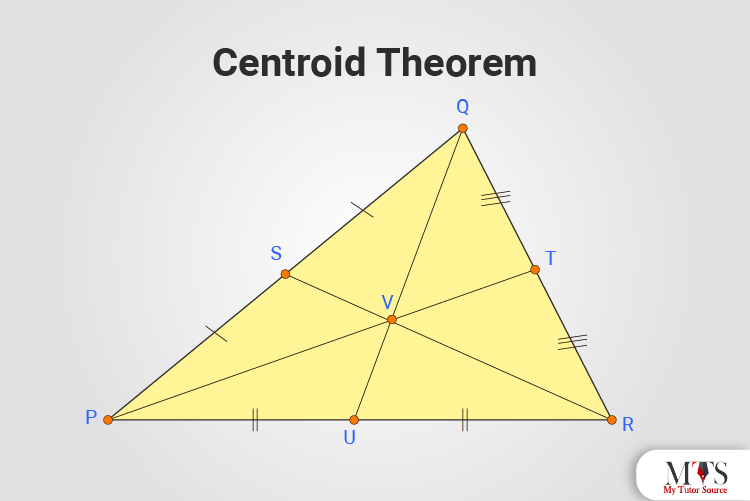
This point is the centroid. It is the point of intersection of all the three medians of a triangle. The centroid divides each median in a ratio of 2:1. The lines will intersect at the centroid. It is formed by the intersection of the medians.

How to Draw the Centroid of a Triangle Construction 21 YouTube

The properties of a centroid are as follows: In every triangle, the centroid is always inside the triangle! To find the centroid, we find the midpoint of two sides in the. Given below is a triangle δabc, where three medians ae, bf, and cd meet at g to from the centriod of the triangle. Web there are a few different.

What is the centroid of a triangle? [Solved]

Learn how to construct the centroid of a triangle by using a compass to construct the medians of the triangle. Let's start with side ab. (you can draw in the third median if you like, but you don’t need it to find the centroid.) now, using something with a small, flat. Web draw a line segment (called the altitude) at.

Centroid of a Triangle Brilliant Math & Science Wiki

The segment you just created is called a median. At the point of intersection (centroid), each median in a triangle is divided in the ratio of 2: The lines will intersect at the centroid. To find the centroid, we find the midpoint of two sides in the. In this article, we discussed the centroid of a triangle, its formula, derivations,.

How to find the centroid of a triangle? Step by step Neurochispas

In this article, we discussed the centroid of a triangle, its formula, derivations, the difference between orthocenter and centroid, and some facts and examples related to the centroid of a triangle. One way is to draw lines from each vertex (corner) of the triangle to the midpoint of the opposite side. Web each of these shapes will have a centroid.

How to construct centroid of a right angle triangle. shsirclasses

Learn about the many centers of a triangle such as centroid, circumcenter and more. In other words, the centroid will always be 2/3 of the way along. Let's start with side ab. It is one of the points of concurrency of a triangle. The intersection point of these medians is the centroid of your triangle.

Centroid of a Triangle Definition, Differences, Properties, Examples

Carefully find the midpoints of two of the sides, and then draw the two medians to those midpoints. Each of these simple shapes is something we have listed in the centroid table to the right. The centroid of a triangle is the point at which the three medians intersect. Let's start with side ab. In this article, we discussed the.

Centroid of a Triangle Definition, Properties, Formulas

Learn about the many centers of a triangle such as centroid, circumcenter and more. The centroid of a triangle is the point where its medians intersect. It is also the center of gravity of the triangle and one of the triangle's points of concurrency. Web it is the point where all 3 medians intersect and is often described as the.

Centroid of a Triangle Brilliant Math & Science Wiki

9, then the ratio of areas of these triangles is The coordinates of the centroid are simply the average of the coordinates of the vertices. Also note that e, f and d are the midpoints of sides bc, ac. Web this video shows how to construct the centroid of a triangle by constructing medians. It works by constructing two medians,.

The Segment You Just Created Is Called A Median.

9, then the ratio of areas of these triangles is The sign structure, probably 5 feet (1.5 meter) wide and 8 feet (2.4 meters) high, has a door and is accessible from the roof, warren said. Web it is the point where all 3 medians intersect and is often described as the triangle's center of gravity or as the barycent. This video tutorial will show you the steps and the commands to use in geogebra.

The Centroid Of A Triangle Is The Point Of Concurrency Of Its Medians.

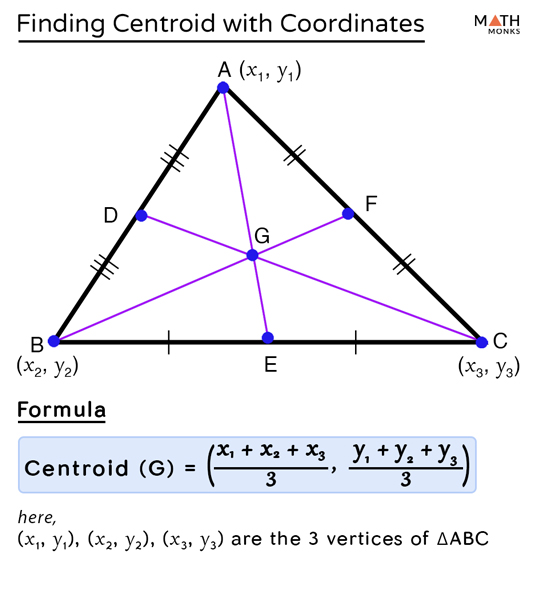
If the coordinates of the vertices of a triangle are (x 1, y 1), (x 2, y 2), (x 3, y 3), then the formula for the centroid of the triangle is given below: Web draw a line segment (called the altitude) at right angles to a side that goes to the opposite corner. Then the orthocenter is also outside the triangle. One way is to draw lines from each vertex (corner) of the triangle to the midpoint of the opposite side.

Each Of These Simple Shapes Is Something We Have Listed In The Centroid Table To The Right.

Choose a side of the triangle. Place a point at the midpoint of one of the sides of the triangle. Web the centroid is the point of concurrency of the three medians in a triangle. It is the point of intersection of all the three medians of a triangle.

Derive The Formulas For The Centroid Location Of The Following Right Triangle.

It is referred to as the center of mass or balance point of the triangle. G (x 1 + x 2 + x 3 / 3 , y 1 + y 2 + y 3 / 3) suggested reference article,. The construction uses only a compass and straight edge. For the shape shown at the top, we can break it down into a rectangle (1), a right triangle (2), and a circular hole (3).