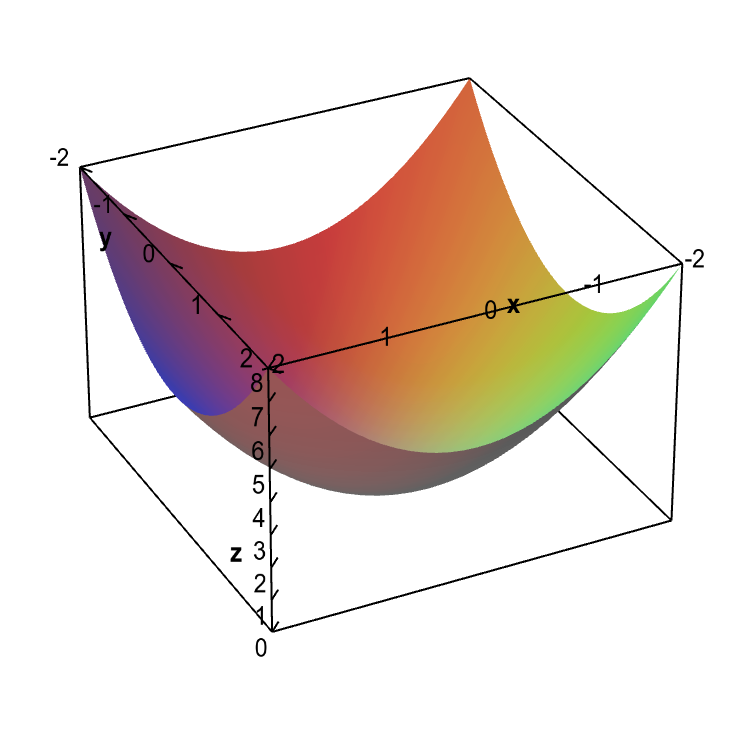How To Draw A Hyperbolic Paraboloid
How To Draw A Hyperbolic Paraboloid - To draw a hyperbolic paraboloid, you can use the following steps: Whatever you use, it needs to be durable enough to withstand being folded and unfolded a number of times. In today's post, we will create a similar model using skewers. \documentclass{article} \usepackage{pgfplots} \begin{document} \begin{figure} \centering. \documentclass[border=5mm]{standalone} \usepackage{tikz} \usetikzlibrary{calc} \begin{document} \begin{tikzpicture}[scale=1,yscale=.5] \draw (0,0) arc (180:0:2); Web draw the hyperbolas one hyperbola for each of the parabolas drawn in planes perpendicular to the axis upper hyperbola drawn with upper parabola the plane is the upper bound for the u variable for this is the plane x = 4 vertices are on the upper parabola lower hyperbola drawn with lower parabola the plane is the lower bound for. 2.5k views 3 years ago. Where ϕ ϕ is our parameter. X2 +y2 to x2 −y2, x 2 + y 2 to x 2 − y 2, we can change from an elliptic paraboloid to a much more complex surface. Web open in matlab online.
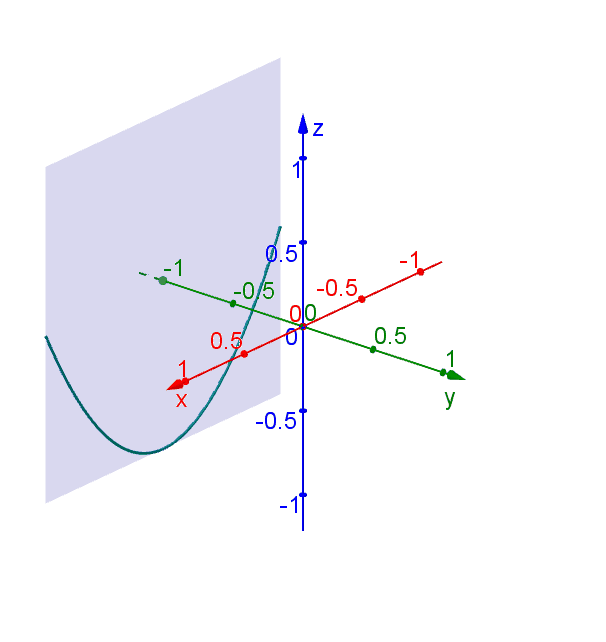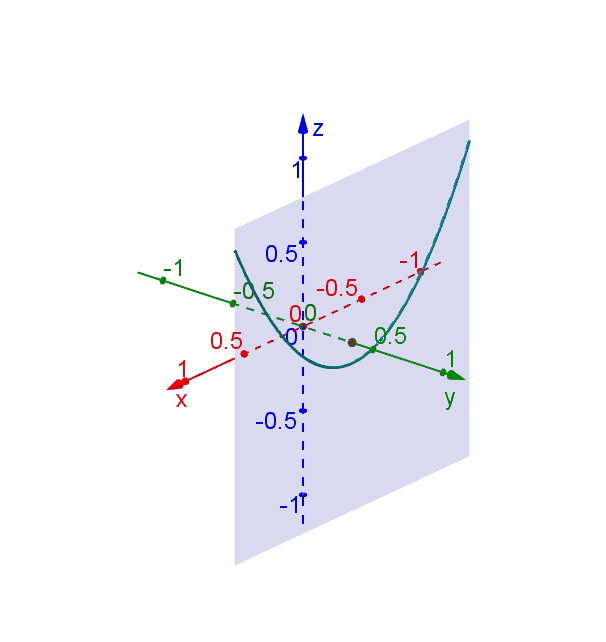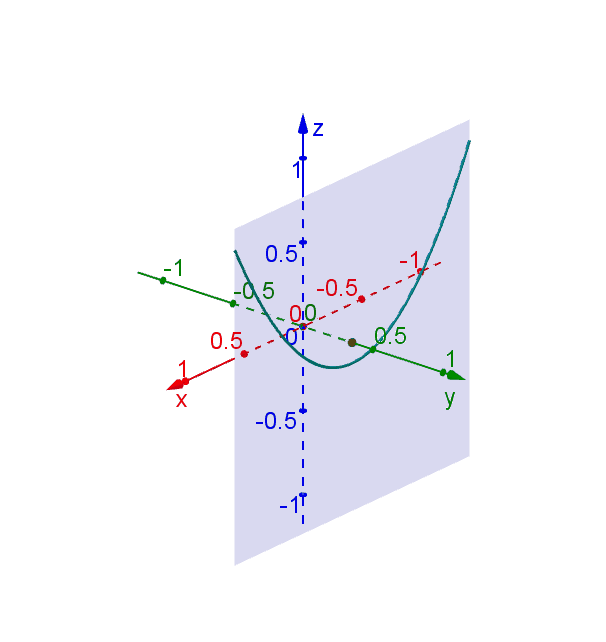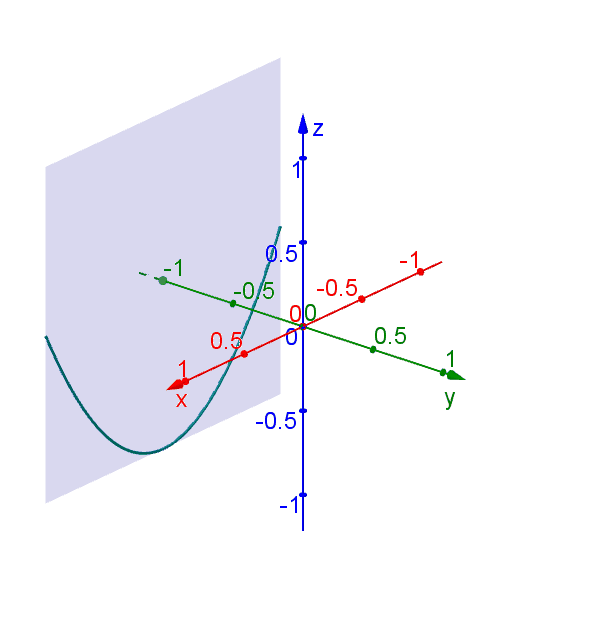
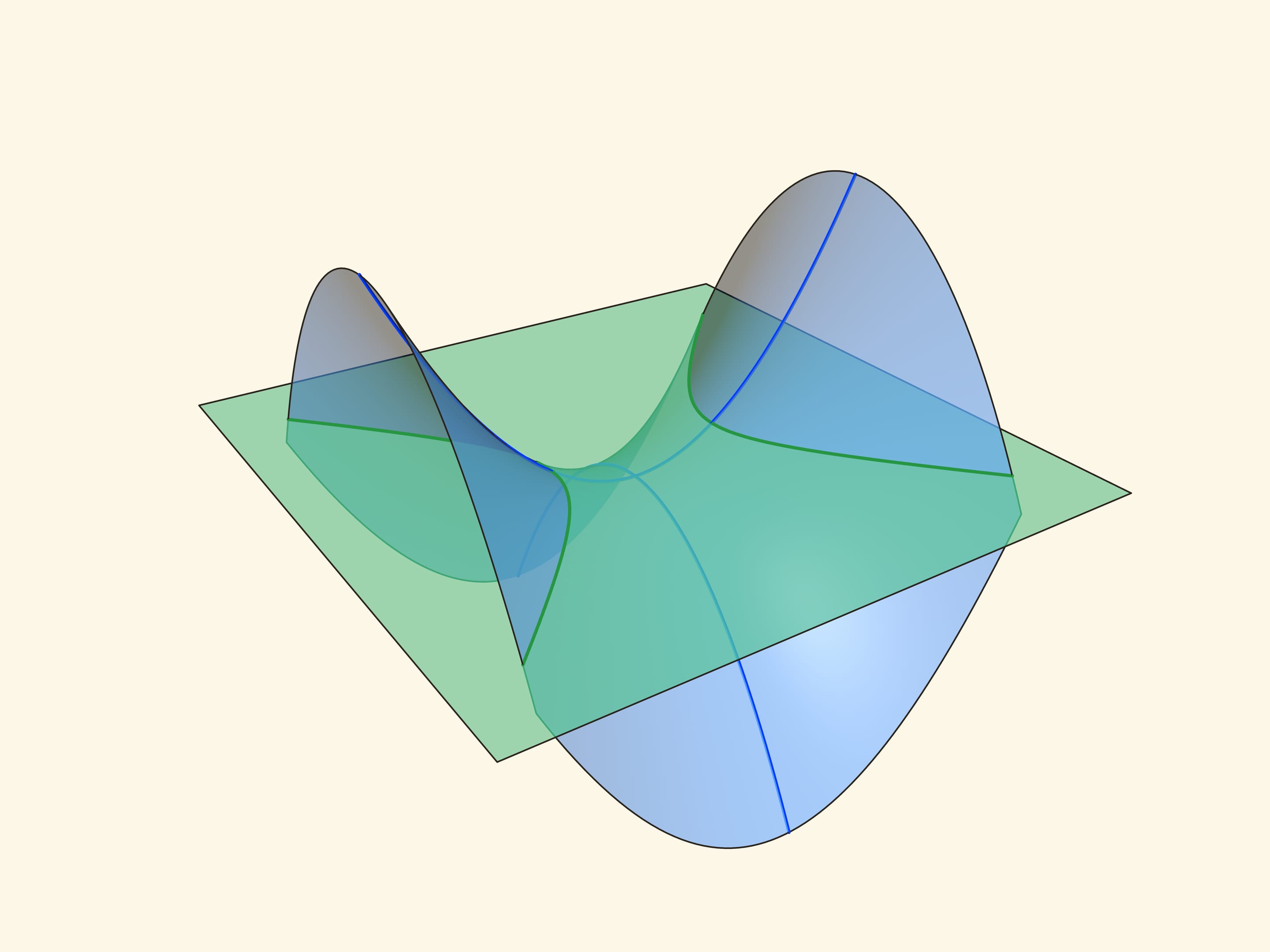
Web drawing a hyperbolic paraboloid. Web how do i draw a hyperbolic paraboloid? Fold and unfold the paper in half. Find the vertices of the hyperbolic paraboloid. Z =x2 −y2 z = x 2 − y 2. Whatever you use, it needs to be durable enough to withstand being folded and unfolded a number of times. Where ϕ ϕ is our parameter. How to draw a hyperbolic paraboloid using two parabolas and two hyperbolas. Web how to plot a hyperbolic paraboloid in a style of the attached figure using only one colour. (where a and b have different signs) with just the flip of a sign, say.
Whatever you use, it needs to be durable enough to withstand being folded and unfolded a number of times. \documentclass[border=5mm]{standalone} \usepackage{tikz} \usetikzlibrary{calc} \begin{document} \begin{tikzpicture}[scale=1,yscale=.5] \draw (0,0) arc (180:0:2); An alternative form is z=xy (2) (right figure; Where ϕ ϕ is our parameter. I'm using a small sheet of gold foil paper, but any origami paper will do. Z =x2 −y2 z = x 2 − y 2. Slices parallel to the x axis and y axis will. Web i am trying to draw a paraboloid using the following code: Most folks find the hyperbolic paraboloid more difficult than the elliptic paraboloid to draw. First things first, you need a sheet of origami paper.
Howto DRAW HYPERBOLIC PARABOLOID (part 4) YouTube
X = k−−√ sec ϕ x = k sec. Find the vertices of the hyperbolic paraboloid. How to draw a hyperbolic paraboloid using two parabolas and two hyperbolas. 2.5k views 3 years ago. Web how to plot a hyperbolic paraboloid in a style of the attached figure using only one colour.
Howto DRAW HYPERBOLIC PARABOLOID (part 2) YouTube
Fold and unfold the paper in half. This video explains how to determine the traces of a hyperbolic. Web how do i draw a hyperbolic paraboloid? (where a and b have different signs) with just the flip of a sign, say. 1 =( x2 k−−√)2 −( y2 k−−√)2 1 = ( x 2 k) 2 − ( y 2 k).
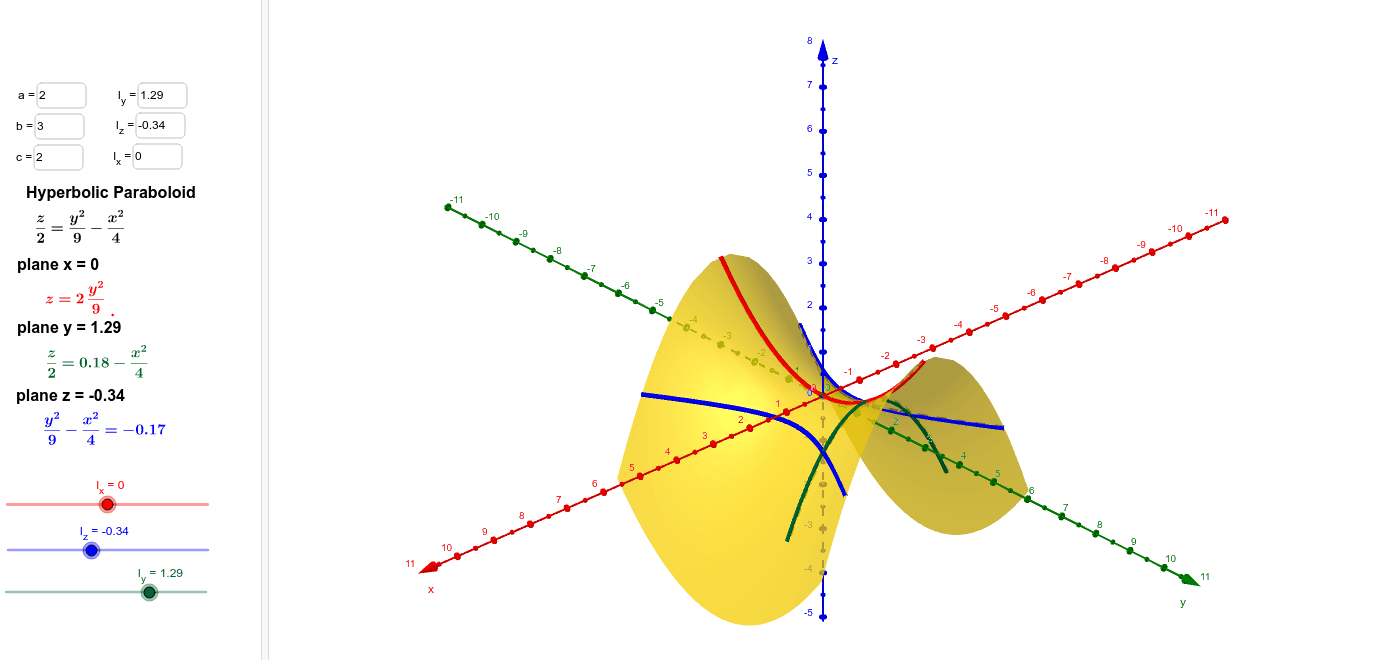
Hyperbolic paraboloid GeoGebra Dynamic Worksheet
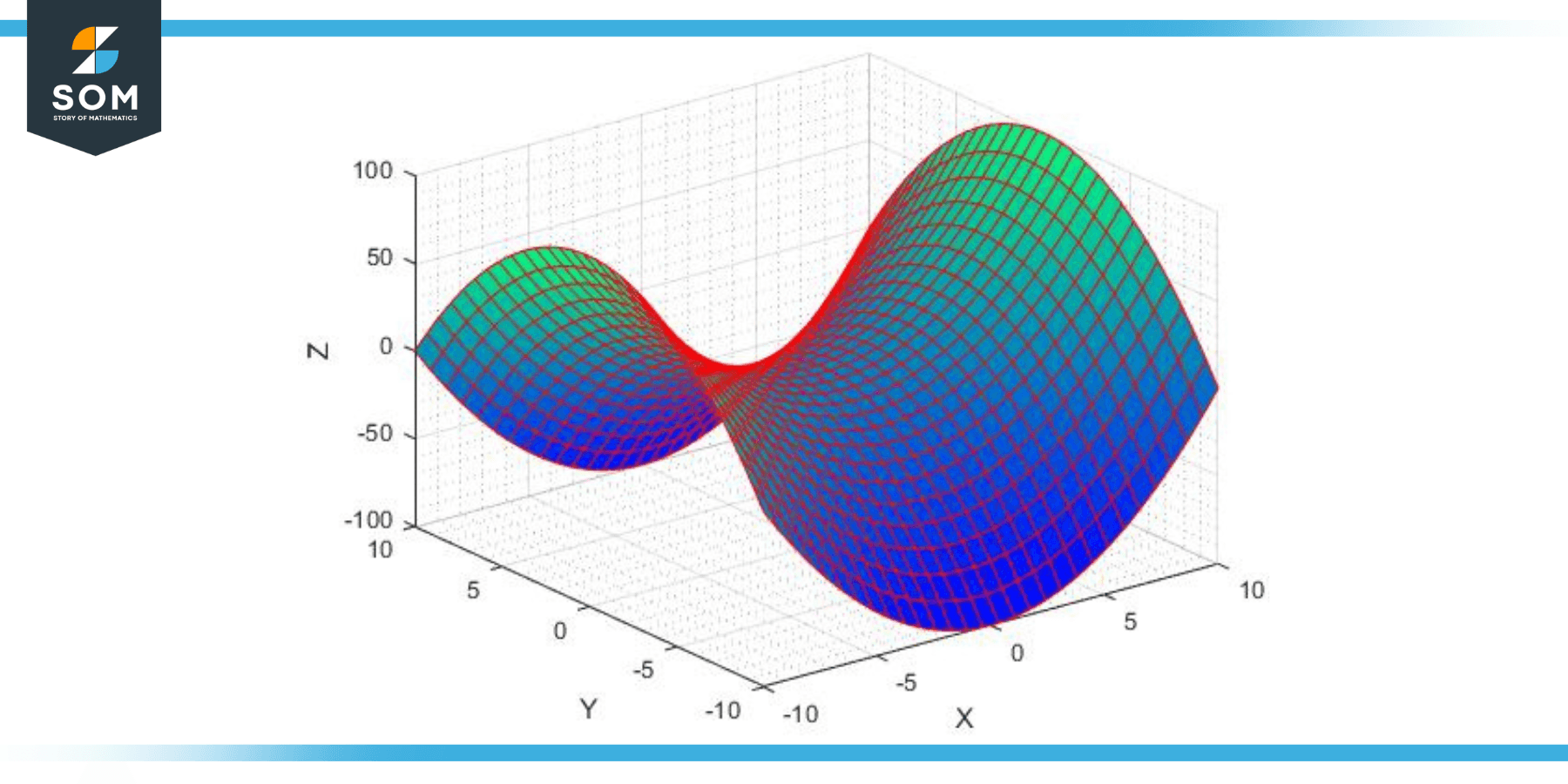
The hyperbolic paraboloid is a ruled surface, which means that you can create it using only straight lines even though it is curved. More detailed diagrams are available. An alternative form is z=xy (2) (right figure; First things first, you need a sheet of origami paper. Web i am trying to draw a paraboloid using the following code:
Saddle surface of a hyperbolic paraboloid / Models // Mathematical Etudes
This video explains how to construct a hyperbola in autocad when the ratio of eccentricity is given. Web how do i draw a hyperbolic paraboloid? As long as you have the mathematical equation describing that hyperboloid, you should be able to generate some data and then draw it. First things first, you need a sheet of origami paper. Web how.
Detail How To Draw Hyperbolic Paraboloid Koleksi Nomer 15
Graph the equation of the hyperbolic paraboloid. More detailed diagrams are available. Web learn how to draw an elliptic and a hyperbolic paraboloid. At this point, there are two basic surfaces that you should get to know quite well: This video explains how to construct a hyperbola in autocad when the ratio of eccentricity is given.
How To Draw A Hyperbolic Paraboloid PDF Manifold Differential
Web make a hyperbolic paraboloid using skewers. Graph the equation of the hyperbolic paraboloid. There are many ways to glue hypars together. Find the vertices of the hyperbolic paraboloid. Most folks find the hyperbolic paraboloid more difficult than the elliptic paraboloid to draw.
How to draw a hyperbolic paraboloid John Ganci
There are many ways to glue hypars together. Whatever you use, it needs to be durable enough to withstand being folded and unfolded a number of times. Web drawing a hyperbolic paraboloid. First things first, you need a sheet of origami paper. As long as you have the mathematical equation describing that hyperboloid, you should be able to generate some.
Hyperbolic paraboloid GeoGebra Dynamic Worksheet
In monday's post, we created a sliceform model of a hyperbolic paraboloid. There are many ways to glue hypars together. Web learn how to draw an elliptic and a hyperbolic paraboloid. As long as you have the mathematical equation describing that hyperboloid, you should be able to generate some data and then draw it. 1 =( x2 k−−√)2 −( y2.
The Hyperbolic ParaboloidDefinition, Geometry With Examples
Z =x2 −y2 z = x 2 − y 2. Web draw the hyperbolas one hyperbola for each of the parabolas drawn in planes perpendicular to the axis upper hyperbola drawn with upper parabola the plane is the upper bound for the u variable for this is the plane x = 4 vertices are on the upper parabola lower hyperbola.
Detail How To Draw Hyperbolic Paraboloid Koleksi Nomer 1
I'm using a small sheet of gold foil paper, but any origami paper will do. Web © 2024 google llc. If you carefully set the mesh grid for x and y, then you can calculate the corresponding value for z. Web open in matlab online. \documentclass[border=5mm]{standalone} \usepackage{tikz} \usetikzlibrary{calc} \begin{document} \begin{tikzpicture}[scale=1,yscale=.5] \draw (0,0) arc (180:0:2);
To Draw A Hyperbolic Paraboloid, You Can Use The Following Steps:
(where a and b have different signs) with just the flip of a sign, say. Z = ax2 + by2 z = a x 2 + b y 2. First things first, you need a sheet of origami paper. Whatever you use, it needs to be durable enough to withstand being folded and unfolded a number of times.
It's A Common Trick When You Are Dealing With Second Powers.
Slices parallel to the x axis and y axis will. As long as you have the mathematical equation describing that hyperboloid, you should be able to generate some data and then draw it. Time to teach you the tricks of the trade. Graph the equation of the hyperbolic paraboloid.
Web Make A Hyperbolic Paraboloid Using Skewers.
Fischer 1986), which has parametric equations x(u,v) = u (3) y(u,v) = v (4) z(u,v) = uv (5) (gray 1997, pp. Web © 2024 google llc. In the first case, you divide whole the equation by k k to get: \begin{tikzpicture} \begin{axis}[ xlabel=$x$, ylabel=$y$, zlabel=$z$, view={60}{30}, ]
Web Drawing A Hyperbolic Paraboloid.
\documentclass[border=5mm]{standalone} \usepackage{tikz} \usetikzlibrary{calc} \begin{document} \begin{tikzpicture}[scale=1,yscale=.5] \draw (0,0) arc (180:0:2); Web how do i draw a hyperbolic paraboloid? When you cut a hyperbolic paraboloid with a circular cutter, the outside edge is two cycles of a cos/sin curve. Web draw the hyperbolas one hyperbola for each of the parabolas drawn in planes perpendicular to the axis upper hyperbola drawn with upper parabola the plane is the upper bound for the u variable for this is the plane x = 4 vertices are on the upper parabola lower hyperbola drawn with lower parabola the plane is the lower bound for.