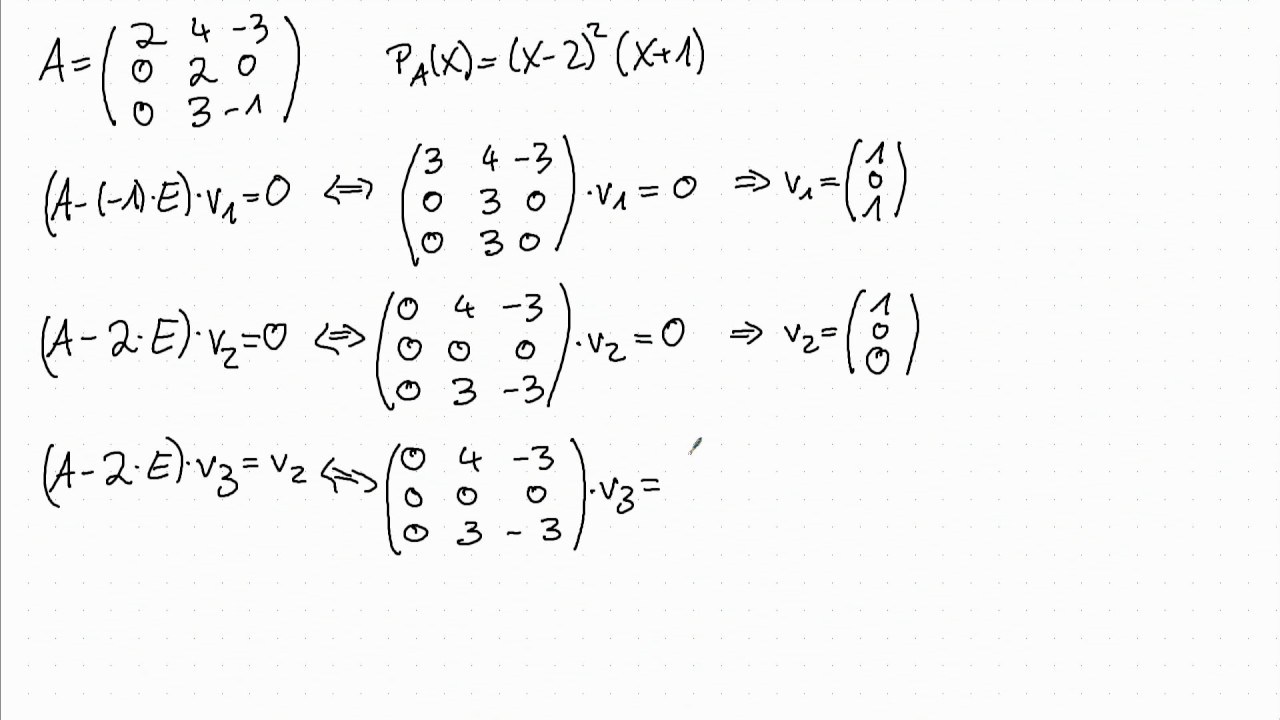Jordan Form Matlab
Jordan Form Matlab - So i also tried [v,d]=eig (sym (a)), and found eig () is much faster than jordan (). Web i want to compute jordan normal form of big circular matrix in matlab (i.e order of 365 x 365) for an example a 4x4 circular matrix has the form : For a given matrix a , find a. Web error in sym/jordan (line 32) [vsym,jsym] = mupadmexnout('symobj::jordan',a,'all'); Web matlab® provides a very useful command to calculate the jordan canonical forms of matrices. R = rref (a,tol) specifies a pivot tolerance that the. Web the jordan canonical form (jordan normal form) results from attempts to convert a matrix to its diagonal form by a similarity transformation. Any operator t on v can be represented by a matrix in jordan form. Web a jordan form is a block diagonal matrix consisting of several jordan blocks. For a given matrix a , find a.
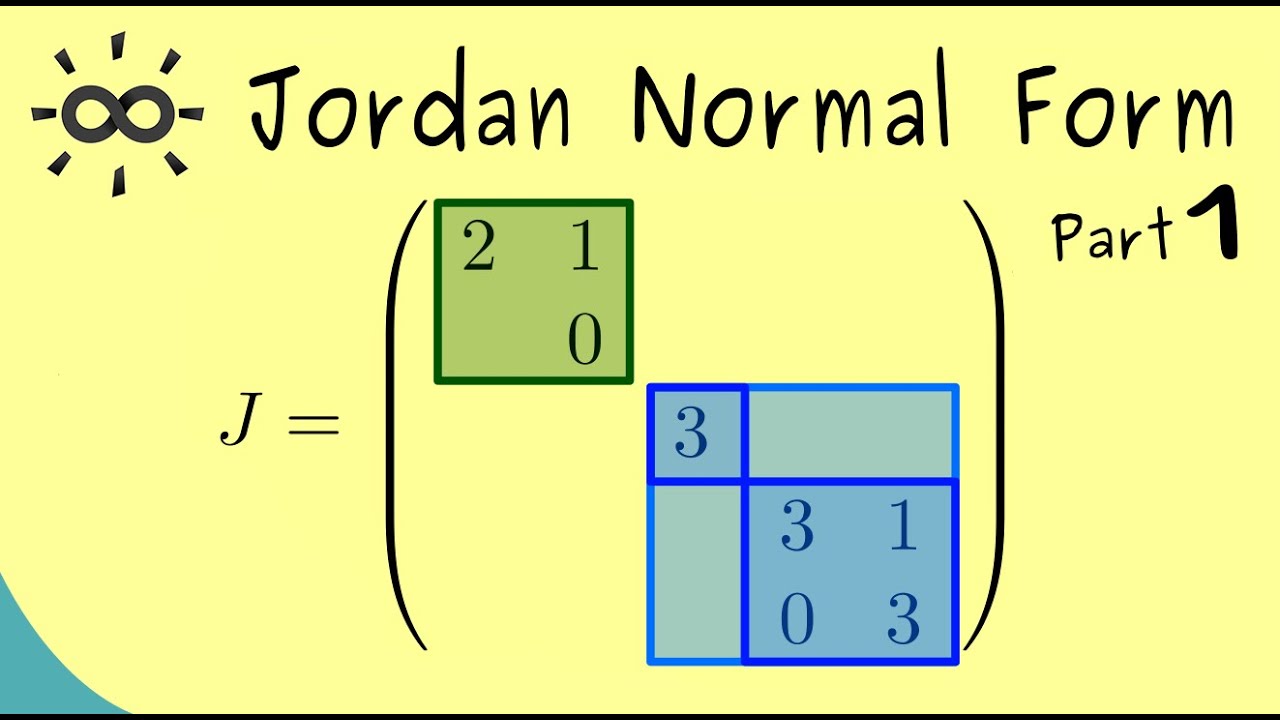
Web error in sym/jordan (line 32) [vsym,jsym] = mupadmexnout('symobj::jordan',a,'all'); Because the jordan form of a numeric matrix is sensitive to numerical errors, prefer converting. So, why doesn't matlab use the jcf in any of its computations?. Web matlab® provides a very useful command to calculate the jordan canonical forms of matrices. This command is called ‘jordan ()’. You can learn matlab® in. For a given matrix a , find a. For example, we can form a jordan form from two copies of j2(4) and one copy of j4(−1 2). Any operator t on v can be represented by a matrix in jordan form. A = [0 1 0 0 ;
Web i want to compute jordan normal form of big circular matrix in matlab (i.e order of 365 x 365) for an example a 4x4 circular matrix has the form : Web matlab® provides a very useful command to calculate the jordan canonical forms of matrices. For example, we can form a jordan form from two copies of j2(4) and one copy of j4(−1 2). You can learn matlab® in. So, why doesn't matlab use the jcf in any of its computations?. Any operator t on v can be represented by a matrix in jordan form. Web a jordan form is a block diagonal matrix consisting of several jordan blocks. This matrix is unique up to a rearrangement of the order of the jordan blocks, and is called the. Because the jordan form of a numeric matrix is sensitive to numerical errors, prefer converting. For a given matrix a , find a.
3.8 Gauss Jordan Elimination with Pivoting (Gaussian Elimination) in
A = [0 1 0 0 ; For example, we can form a jordan form from two copies of j2(4) and one copy of j4(−1 2). Web a jordan form is a block diagonal matrix consisting of several jordan blocks. Web error in sym/jordan (line 32) [vsym,jsym] = mupadmexnout('symobj::jordan',a,'all'); For a given matrix a , find a.
Calculating the Jordan form of a matrix SciPy Recipes
Web i want to compute jordan normal form of big circular matrix in matlab (i.e order of 365 x 365) for an example a 4x4 circular matrix has the form : For a given matrix a , find a. R = rref (a,tol) specifies a pivot tolerance that the. Web the jordan canonical form (jordan normal form) results from attempts.
Breanna Jordan Normal Form Matlab
Web a jordan form is a block diagonal matrix consisting of several jordan blocks. Any operator t on v can be represented by a matrix in jordan form. J = jordan (a) computes the jordan normal form of the matrix a. Because the jordan form of a numeric matrix is sensitive to numerical errors, prefer converting. For a given matrix.
Jordan form YouTube
Web the jordan canonical form (jordan normal form) results from attempts to convert a matrix to its diagonal form by a similarity transformation. Any operator t on v can be represented by a matrix in jordan form. Web the jordan canonical form (jordan normal form) results from attempts to convert a matrix to its diagonal form by a similarity transformation..
Breanna Jordan Normal Form Proof
Web error in sym/jordan (line 32) [vsym,jsym] = mupadmexnout('symobj::jordan',a,'all'); Web matlab always returns the matrix j sorting the diagonal from lowest to highest, until it encounters repeated eigenvalue (s), which are sorted in jordan blocks in. J = jordan (a) computes the jordan normal form of the matrix a. For a given matrix a , find a. You can learn.
Jordan Form YouTube
This command is called ‘jordan ()’. Web matlab® provides a very useful command to calculate the jordan canonical forms of matrices. A = [0 1 0 0 ; Web the jordan canonical form (jordan normal form) results from attempts to convert a matrix to its diagonal form by a similarity transformation. For example, we can form a jordan form from.
LAII 009 Example of a Jordan normal form YouTube
Web in linear algebra, a jordan normal form, also known as a jordan canonical form (jcf), is an upper triangular matrix of a particular form called a jordan matrix representing a linear. Web the jordan canonical form (jordan normal form) results from attempts to convert a matrix to its diagonal form by a similarity transformation. Web the jordan canonical form.
LA Sec 10.1 Finding the Jordan Canonical Form with a Dot Diagram YouTube
Web the jordan canonical form (jordan normal form) results from attempts to convert a matrix to its diagonal form by a similarity transformation. Web in linear algebra, a jordan normal form, also known as a jordan canonical form (jcf), is an upper triangular matrix of a particular form called a jordan matrix representing a linear. Web error in sym/jordan (line.
Jordan Form YouTube
R = rref (a,tol) specifies a pivot tolerance that the. Web matlab® provides a very useful command to calculate the jordan canonical forms of matrices. Web the jordan canonical form (jordan normal form) results from attempts to convert a matrix to its diagonal form by a similarity transformation. For example, we can form a jordan form from two copies of.
Jordan Normal Form Part 1 Overview YouTube
You can learn matlab® in. Web the jordan canonical form (jordan normal form) results from attempts to convert a matrix to its diagonal form by a similarity transformation. For a given matrix a , find a. A = [0 1 0 0 ; For a given matrix a , find a.
I've Read In The Matlab Help That Computation Of The Jordan Form Is Very Sensitive To.
Web a jordan form is a block diagonal matrix consisting of several jordan blocks. This command is called ‘jordan ()’. So, why doesn't matlab use the jcf in any of its computations?. So i also tried [v,d]=eig (sym (a)), and found eig () is much faster than jordan ().
For A Given Matrix A , Find A.
For example, we can form a jordan form from two copies of j2(4) and one copy of j4(−1 2). Web the jordan canonical form (jordan normal form) results from attempts to convert a matrix to its diagonal form by a similarity transformation. Web the jordan canonical form (jordan normal form) results from attempts to convert a matrix to its diagonal form by a similarity transformation. For a given matrix a , find a.
You Can Learn Matlab® In.
A = [0 1 0 0 ; Web error in sym/jordan (line 32) [vsym,jsym] = mupadmexnout('symobj::jordan',a,'all'); Web the jordan canonical form is the key relationship between matrices and differential equations. Web jordan form lds consider lds x˙ = ax by change of coordinates x = tx˜, can put into form x˜˙ = jx˜ system is decomposed into independent ‘jordan block systems’ x˜˙ i = jix˜i x˜n.
Web Matlab® Provides A Very Useful Command To Calculate The Jordan Canonical Forms Of Matrices.
Web the jordan canonical form (jordan normal form) results from attempts to convert a matrix to its diagonal form by a similarity transformation. Web the jordan canonical form (jordan normal form) results from attempts to convert a matrix to its diagonal form by a similarity transformation. For a given matrix a, find a. This matrix is unique up to a rearrangement of the order of the jordan blocks, and is called the.