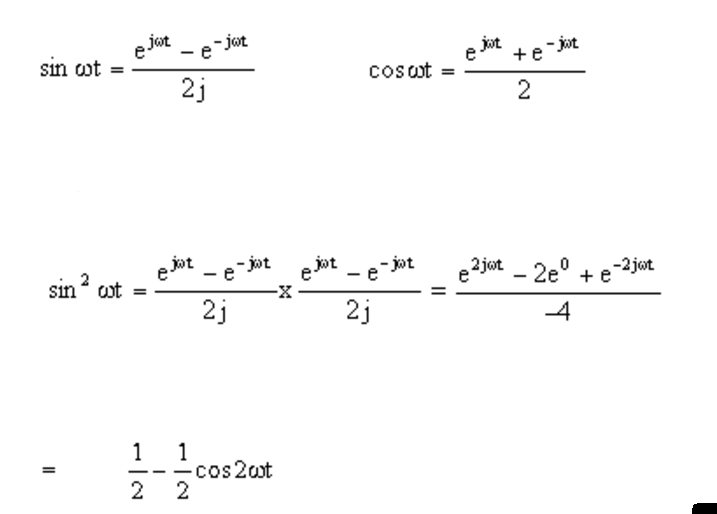
Sine And Cosine In Exponential Form

Sine And Cosine In Exponential Form - Web we can use euler’s theorem to express sine and cosine in terms of the complex exponential function as s i n c o s 𝜃 = 1 2 𝑖 𝑒 − 𝑒 , 𝜃 = 1 2 𝑒 + 𝑒. This formula can be interpreted as saying that the function e is a unit complex number, i.e., it traces out the unit circle in the complex plane as φ ranges through the real numbers. (10) in other words, a = − √ a2 + b2, φ = tan 1(b/a). Using these formulas, we can. A cos(λt)+ b sin(λt) = re ((a − bi)· (cos(λt)+ i. Web answer (1 of 3): I think they are phase shifting the euler formula 90 degrees with the j at the front since the real part of euler is given in terms of cosine but. Periodicity of the imaginary exponential. Inverse trigonometric functions are useful when trying to determine the remaining two angles of a right triangle when the. Here φ is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radians.

Web in complex analysis, the hyperbolic functions arise when applying the ordinary sine and cosine functions to an imaginary angle. To prove (10), we have: Web according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and sin(t) via the following inspired definition: Using these formulas, we can. Web notes on the complex exponential and sine functions (x1.5) i. The hyperbolic sine and the hyperbolic cosine. Web 1 answer sorted by: Web answer (1 of 3): Web feb 22, 2021 at 14:40. I think they are phase shifting the euler formula 90 degrees with the j at the front since the real part of euler is given in terms of cosine but.

Web feb 22, 2021 at 14:40. I think they are phase shifting the euler formula 90 degrees with the j at the front since the real part of euler is given in terms of cosine but. Web we can use euler’s theorem to express sine and cosine in terms of the complex exponential function as s i n c o s 𝜃 = 1 2 𝑖 𝑒 − 𝑒 , 𝜃 = 1 2 𝑒 + 𝑒. Web integrals of the form z cos(ax)cos(bx)dx; The hyperbolic sine and the hyperbolic cosine. This formula can be interpreted as saying that the function e is a unit complex number, i.e., it traces out the unit circle in the complex plane as φ ranges through the real numbers. Web notes on the complex exponential and sine functions (x1.5) i. Z cos(ax)sin(bx)dx or z sin(ax)sin(bx)dx are usually done by using the addition formulas for the cosine and sine functions. (10) in other words, a = − √ a2 + b2, φ = tan 1(b/a). Inverse trigonometric functions are useful when trying to determine the remaining two angles of a right triangle when the.

Sine and cosine problems Math Tutoring & Exercises

A cos(λt)+ b sin(λt) = re ((a − bi)· (cos(λt)+ i. A real exponential function is not related to sinusoids…and although u can use a real cosine signal to pass it thru hilbert transformer to get a. The hyperbolic sine and the hyperbolic cosine. Web answer (1 of 3): Inverse trigonometric functions are useful when trying to determine the remaining.

complex numbers Converting i to exponential form Mathematics

A cos(λt)+ b sin(λt) = re ((a − bi)· (cos(λt)+ i. Web according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and sin(t) via the following inspired definition: Web notes on the complex exponential and sine functions (x1.5) i. Web in complex analysis, the hyperbolic functions arise when applying the ordinary sine.

EM to Optics 10 Converting Cos & Sine to Complex Exponentials YouTube

Here φ is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radians. Sin ⁡ x = e i x − e − i x 2 i cos ⁡ x = e i x + e − i x 2. Web we can use.

Question Video Converting the Product of Complex Numbers in Polar Form

A real exponential function is not related to sinusoids…and although u can use a real cosine signal to pass it thru hilbert transformer to get a. A cos(λt)+ b sin(λt) = re ((a − bi)· (cos(λt)+ i. Web we can use euler’s theorem to express sine and cosine in terms of the complex exponential function as s i n c.

Solved 31. Determine the equation for a) COSINE function

Web solving this linear system in sine and cosine, one can express them in terms of the exponential function: The hyperbolic sine and the hyperbolic cosine. Z cos(ax)sin(bx)dx or z sin(ax)sin(bx)dx are usually done by using the addition formulas for the cosine and sine functions. Using these formulas, we can. Web feb 22, 2021 at 14:40.

Function For Sine Wave Between Two Exponential Cuves Mathematics

Web feb 22, 2021 at 14:40. This formula can be interpreted as saying that the function e is a unit complex number, i.e., it traces out the unit circle in the complex plane as φ ranges through the real numbers. Web 1 answer sorted by: Using these formulas, we can. Web today, we derive the complex exponential definitions of the.

Other Math Archive January 29, 2018

Here φ is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radians. Web notes on the complex exponential and sine functions (x1.5) i. Web today, we derive the complex exponential definitions of the sine and cosine function, using euler's formula. I think they.

Write Equations Of Sine Functions Using Properties Calculator

Web today, we derive the complex exponential definitions of the sine and cosine function, using euler's formula. Web notes on the complex exponential and sine functions (x1.5) i. Web in complex analysis, the hyperbolic functions arise when applying the ordinary sine and cosine functions to an imaginary angle. A real exponential function is not related to sinusoids…and although u can.

Relationship between sine, cosine and exponential function

Inverse trigonometric functions are useful when trying to determine the remaining two angles of a right triangle when the. Web solving this linear system in sine and cosine, one can express them in terms of the exponential function: Web answer (1 of 3): Sin ⁡ x = e i x − e − i x 2 i cos ⁡ x.

Basics of QPSK modulation and display of QPSK signals Electrical

Web answer (1 of 3): Web notes on the complex exponential and sine functions (x1.5) i. Web integrals of the form z cos(ax)cos(bx)dx; Web feb 22, 2021 at 14:40. A cos(λt)+ b sin(λt) = re ((a − bi)· (cos(λt)+ i.

Web Notes On The Complex Exponential And Sine Functions (X1.5) I.

Web we can use euler’s theorem to express sine and cosine in terms of the complex exponential function as s i n c o s 𝜃 = 1 2 𝑖 𝑒 − 𝑒 , 𝜃 = 1 2 𝑒 + 𝑒. A real exponential function is not related to sinusoids…and although u can use a real cosine signal to pass it thru hilbert transformer to get a. Web a right triangle with sides relative to an angle at the point. Web answer (1 of 3):

Web 1 Answer Sorted By:

(10) in other words, a = − √ a2 + b2, φ = tan 1(b/a). Web today, we derive the complex exponential definitions of the sine and cosine function, using euler's formula. To prove (10), we have: Periodicity of the imaginary exponential.

Web Feb 22, 2021 At 14:40.

Web a cos(λt)+ b sin(λt) = a cos(λt − φ), where a + bi = aeiφ; The hyperbolic sine and the hyperbolic cosine. Eix = cos x + i sin x e i x = cos x + i sin x, and e−ix = cos(−x) + i sin(−x) = cos x − i sin x e − i x = cos ( − x) + i sin ( − x) = cos x − i sin. Web in complex analysis, the hyperbolic functions arise when applying the ordinary sine and cosine functions to an imaginary angle.

Sin ⁡ X = E I X − E − I X 2 I Cos ⁡ X = E I X + E − I X 2.

Here φ is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radians. A cos(λt)+ b sin(λt) = re ((a − bi)· (cos(λt)+ i. Web integrals of the form z cos(ax)cos(bx)dx; Web according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and sin(t) via the following inspired definition: