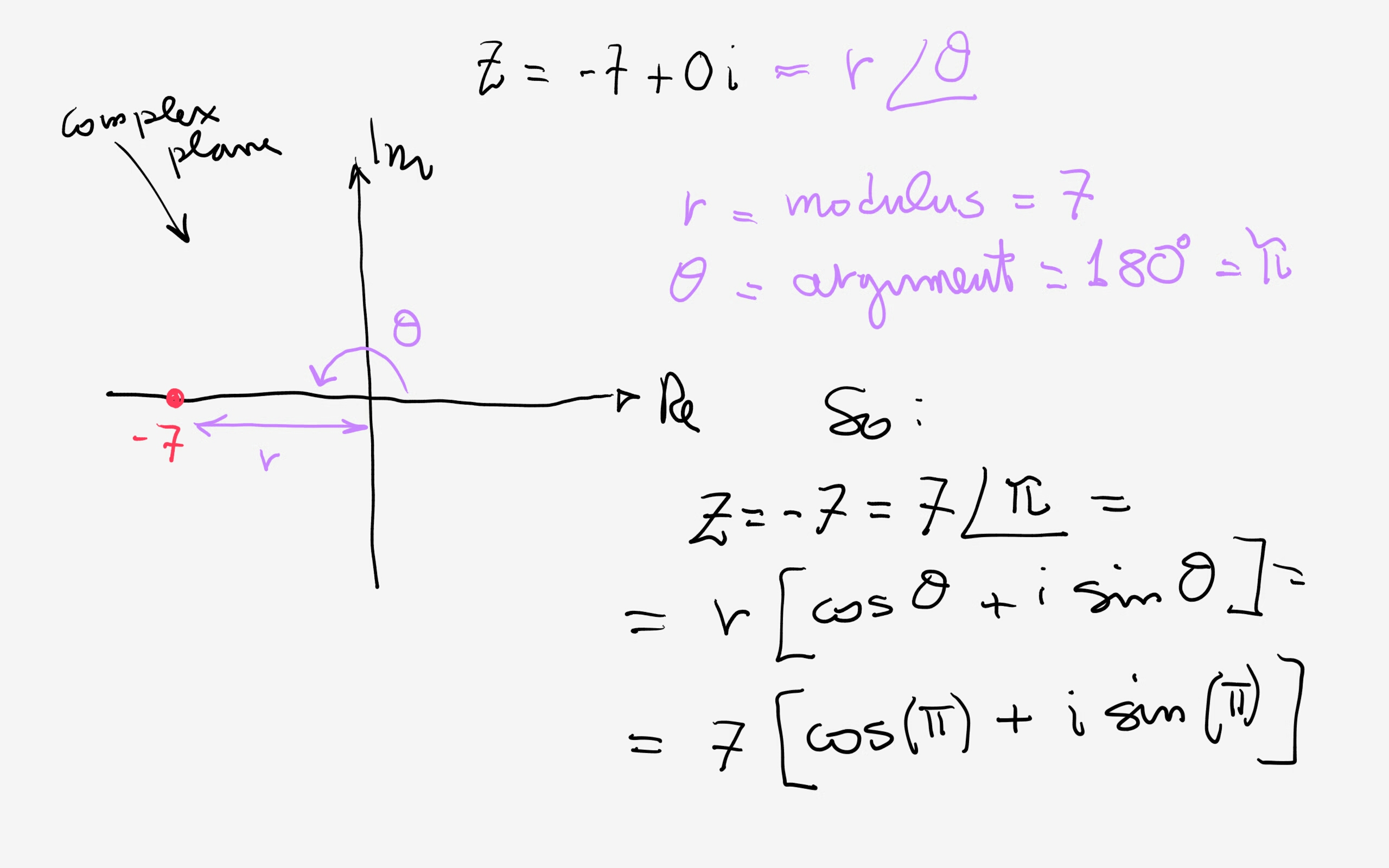Trigonometric Form Of Complex Numbers

Trigonometric Form Of Complex Numbers - Web trigonometric polar form of a complex number describes the location of a point on the complex plane using the angle and the radius of the point. 4 + 4i to write the number in trigonometric form, we needrand. Web euler's formula states that for any real number x : Let's compute the two trigonometric forms: Where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively. This complex exponential function is sometimes denoted cis x (cosine plus i sine). Quotients of complex numbers in polar form. Put these complex numbers in trigonometric form. For example, let z1 = 1 + i, z2 = √3 +i and z3 = −1 +i√3. There is an important product formula for complex numbers that the polar form.

For example, let z1 = 1 + i, z2 = √3 +i and z3 = −1 +i√3. From the graph, we can see how the trigonometric or polar forms of complex numbers were derived. There is an important product formula for complex numbers that the polar form. 4 + 4i to write the number in trigonometric form, we needrand. You will use the distance from the point to the origin as r and the angle that the point makes as \(\theta \). Let's compute the two trigonometric forms: Web euler's formula states that for any real number x : This is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex plane. Quotients of complex numbers in polar form. Where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively.

Web the trigonometric form of a complex number contains the modulus, r, and the argument, θ, representing the complex number. = a + bi becomes z = r(cos + isin ) = |z| and the reference angle, ' is given by tan ' = |b/a| note that it is up to you to make sure is in the correct quadrant. Where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively. Put these complex numbers in trigonometric form. This complex exponential function is sometimes denoted cis x (cosine plus i sine). 4 + 4i to write the number in trigonometric form, we needrand. This is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex plane. Normally,we will require 0 complex numbers in trigonometric form: Web why do you need to find the trigonometric form of a complex number? Ppp =16 + 16 =32 = 42 4 tan ==1 43 =;

PPT 10.4 Trigonometric (Polar) Form of Complex Numbers PowerPoint

Web why do you need to find the trigonometric form of a complex number? This is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex plane. The trigonometric form of a complex number products of complex numbers in polar form. There is an important.

PPT Trigonometric Form of a Complex Number PowerPoint Presentation

Web trigonometric form of a complex number. We have seen that we multiply complex numbers in polar form by multiplying. 4 + 4i to write the number in trigonometric form, we needrand. Normally,we will require 0 complex numbers in trigonometric form: You will use the distance from the point to the origin as r and the angle that the point.

PPT Trigonometric Form of a Complex Number PowerPoint Presentation

Web thetrigonometric formof a complex numberz=a+biis =r(cos +isin ); Where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively. Ppp =16 + 16 =32 = 42 4 tan ==1 43 =; Web trigonometric polar form of a complex number describes the location of a.

Trigonometric Form Into A Complex Number

The trigonometric form of a complex number products of complex numbers in polar form. Bwherer=ja+bij is themodulusofz, and tan =a. Web trigonometric form of a complex number. This complex exponential function is sometimes denoted cis x (cosine plus i sine). Normally,we will require 0 complex numbers in trigonometric form:

PPT Trigonometric Form of a Complex Number PowerPoint Presentation

Normally,we will require 0 complex numbers in trigonometric form: From the graph, we can see how the trigonometric or polar forms of complex numbers were derived. Web thetrigonometric formof a complex numberz=a+biis =r(cos +isin ); Web trigonometric polar form of a complex number describes the location of a point on the complex plane using the angle and the radius of.

How do you express the complex number in trigonometric form 2+(sqrt 3

The trigonometric form of a complex number products of complex numbers in polar form. Where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively. Let's compute the two trigonometric forms: This is the trigonometric form of a complex number where |z| | z |.

PPT Trigonometric Form of a Complex Number PowerPoint Presentation

This is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex plane. You will use the distance from the point to the origin as r and the angle that the point makes as \(\theta \). 4 + 4i to write the number in trigonometric.

Complex Numbers in Trigonometric Form YouTube

Put these complex numbers in trigonometric form. The trigonometric form of a complex number products of complex numbers in polar form. Let's compute the two trigonometric forms: Web why do you need to find the trigonometric form of a complex number? You will use the distance from the point to the origin as r and the angle that the point.

The Product and Quotient of Complex Numbers in Trigonometric Form YouTube

Where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively. Normally,we will require 0 complex numbers in trigonometric form: For example, let z1 = 1 + i, z2 = √3 +i and z3 = −1 +i√3. Web trigonometric polar form of a complex number.

How do you write the complex number in trigonometric form 7? Socratic

Put these complex numbers in trigonometric form. 4 + 4i to write the number in trigonometric form, we needrand. Web trigonometric form of a complex number. Quotients of complex numbers in polar form. Normally,we will require 0 complex numbers in trigonometric form:

We Have Seen That We Multiply Complex Numbers In Polar Form By Multiplying.

This is the trigonometric form of a complex number where |z| | z | is the modulus and θ θ is the angle created on the complex plane. Where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively. The general trigonometric form of complex numbers is r ( cos θ + i sin θ). Put these complex numbers in trigonometric form.

Normally,We Will Require 0 Complex Numbers In Trigonometric Form:

Web the trigonometric form of a complex number contains the modulus, r, and the argument, θ, representing the complex number. This complex exponential function is sometimes denoted cis x (cosine plus i sine). Quotients of complex numbers in polar form. Web trigonometric form of a complex number.

For Example, Let Z1 = 1 + I, Z2 = √3 +I And Z3 = −1 +I√3.

Web euler's formula states that for any real number x : Ppp =16 + 16 =32 = 42 4 tan ==1 43 =; Web trigonometric polar form of a complex number describes the location of a point on the complex plane using the angle and the radius of the point. Let's compute the two trigonometric forms:

= A + Bi Becomes Z = R(Cos + Isin ) = |Z| And The Reference Angle, ' Is Given By Tan ' = |B/A| Note That It Is Up To You To Make Sure Is In The Correct Quadrant.

Web thetrigonometric formof a complex numberz=a+biis =r(cos +isin ); Web why do you need to find the trigonometric form of a complex number? 4 + 4i to write the number in trigonometric form, we needrand. From the graph, we can see how the trigonometric or polar forms of complex numbers were derived.