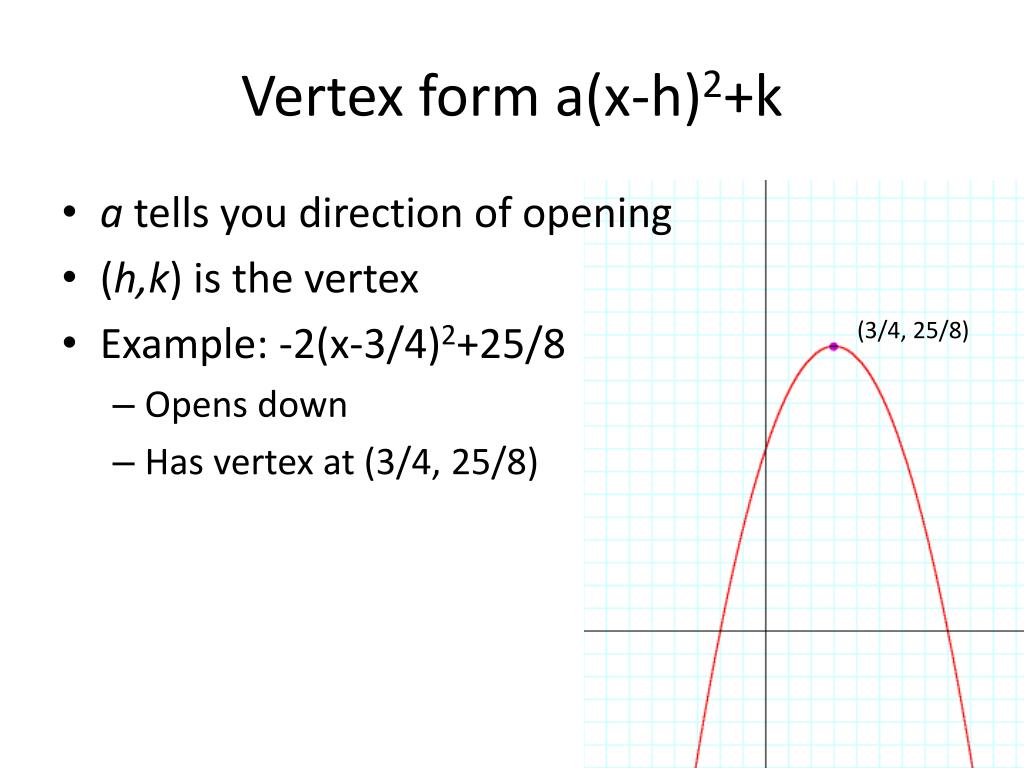
What Is K In Vertex Form
What Is K In Vertex Form - 𝑎 < 0 ⇒ (ℎ, 𝑘) is the maximum point. Graphing a quadratic function in vertex form a graph of a quadratic function with its vertex labeled as (h, k) when graphing a quadratic function with vertex form, the vertex's x and y values are h and k respectively. • (h, k) is the vertex of the parabola, and x = h is the axis of symmetry. 𝑎 > 0 ⇒ (ℎ, 𝑘) is the minimum point. • the h represents a horizontal shift (how far left, or right, the graph has shifted from x = 0). Web with ℎ = −𝑏 ∕ (2𝑎) and 𝑘 = 𝑐 − 𝑏² ∕ (4𝑎) we get. Web when the equation is reformatted as above, the point (h, k) is the vertex. But how to find the vertex of a quadratic function? (a will stay the same, h is x, and k is y). In other words, for the vertex, (x, y) = (h, k).
𝑎 > 0 ⇒ (ℎ, 𝑘) is the minimum point. While the standard quadratic form is a x 2 + b x + c = y, the vertex form of a quadratic equation is y = a ( x − h) 2 + k. Web the vertex form of a parabola's equation is generally expressed as: Y = a ( x − h) 2 + k (h,k) is the vertex as you can see in the picture below if a is positive then the parabola opens upwards like a regular u. Graphing a quadratic function in vertex form a graph of a quadratic function with its vertex labeled as (h, k) when graphing a quadratic function with vertex form, the vertex's x and y values are h and k respectively. That is, both of the a 's have exactly the same value. (𝑥 − ℎ)² ≥ 0 for all 𝑥. • the h represents a horizontal shift (how far left, or right, the graph has shifted from x = 0). Web when the equation is reformatted as above, the point (h, k) is the vertex. (a will stay the same, h is x, and k is y).
• the k represents a vertical shift (how. Web what is vertex form? (a will stay the same, h is x, and k is y). Y = a ( x − h) 2 + k (h,k) is the vertex as you can see in the picture below if a is positive then the parabola opens upwards like a regular u. So the parabola will have a vertex when (𝑥 − ℎ)² = 0 ⇔ 𝑥 = ℎ ⇒ 𝑦 = 𝑘. • (h, k) is the vertex of the parabola, and x = h is the axis of symmetry. While the standard quadratic form is a x 2 + b x + c = y, the vertex form of a quadratic equation is y = a ( x − h) 2 + k. It may be a surprise, but we don't need to evaluate any square root to do so! This is something that we cannot immediately read from the standard form of a quadratic equation. If a is negative, then the.
Formula Quadratic Equation Vertex Form pametno
Web what is vertex form? The sign on a (plus or minus) tells you whether the quadratic's parabola opens up or opens down. It may be a surprise, but we don't need to evaluate any square root to do so! Web with ℎ = −𝑏 ∕ (2𝑎) and 𝑘 = 𝑐 − 𝑏² ∕ (4𝑎) we get. That's enough on.
Standard Form to Vertex Form? With Easy Examples Get Education Bee
But how to find the vertex of a quadratic function? Web when written in vertex form : 𝑦 = 𝑎 (𝑥 − ℎ)² + 𝑘. 𝑎 < 0 ⇒ (ℎ, 𝑘) is the maximum point. • (h, k) is the vertex of the parabola, and x = h is the axis of symmetry.
conic sections History behind the choice of letters h and k for
𝑎 > 0 ⇒ (ℎ, 𝑘) is the minimum point. (a will stay the same, h is x, and k is y). Web the vertex form of a parabola's equation is generally expressed as: It may be a surprise, but we don't need to evaluate any square root to do so! Graphing a quadratic function in vertex form a graph.
Standard Form to Vertex Form Part 2 YouTube
Web what is vertex form? Web the vertex form of a parabola's equation is generally expressed as: • (h, k) is the vertex of the parabola, and x = h is the axis of symmetry. That's enough on the definitions. Graphing a quadratic function in vertex form a graph of a quadratic function with its vertex labeled as (h, k).
PPT Lesson 4.2 , For use with pages 245251 PowerPoint Presentation
𝑎 > 0 ⇒ (ℎ, 𝑘) is the minimum point. • the h represents a horizontal shift (how far left, or right, the graph has shifted from x = 0). 𝑦 = 𝑎 (𝑥 − ℎ)² + 𝑘. 𝑎 < 0 ⇒ (ℎ, 𝑘) is the maximum point. It may be a surprise, but we don't need to evaluate any.
Standard Form To Vertex Form Khan Academy How To Do Vertex Formula
𝑎 > 0 ⇒ (ℎ, 𝑘) is the minimum point. In other words, for the vertex, (x, y) = (h, k). It may be a surprise, but we don't need to evaluate any square root to do so! (𝑥 − ℎ)² ≥ 0 for all 𝑥. That is, both of the a 's have exactly the same value.
The Vertex Formula YouTube
• the h represents a horizontal shift (how far left, or right, the graph has shifted from x = 0). The a in the vertex form is the same a as in y = ax2 + bx + c; (a will stay the same, h is x, and k is y). Web the vertex form of a parabola's equation is.
Graphing Quadratics in Vertex Form Notes YouTube
𝑦 = 𝑎 (𝑥 − ℎ)² + 𝑘. Y = a ( x − h) 2 + k (h,k) is the vertex as you can see in the picture below if a is positive then the parabola opens upwards like a regular u. Web when the equation is reformatted as above, the point (h, k) is the vertex. The sign.
Vertex Form By Completing The Square Writing A Quadratic Function In
• the h represents a horizontal shift (how far left, or right, the graph has shifted from x = 0). That's enough on the definitions. It may be a surprise, but we don't need to evaluate any square root to do so! This is something that we cannot immediately read from the standard form of a quadratic equation. 𝑎 <.
Vertex Form "k" YouTube
(a will stay the same, h is x, and k is y). That's enough on the definitions. • the h represents a horizontal shift (how far left, or right, the graph has shifted from x = 0). Web with ℎ = −𝑏 ∕ (2𝑎) and 𝑘 = 𝑐 − 𝑏² ∕ (4𝑎) we get. Web when the equation is reformatted.
A Is Negative Therefore Will Open Down And Have A Maximum Point.
That's enough on the definitions. • (h, k) is the vertex of the parabola, and x = h is the axis of symmetry. The a in the vertex form is the same a as in y = ax2 + bx + c; 𝑎 > 0 ⇒ (ℎ, 𝑘) is the minimum point.
Web With ℎ = −𝑏 ∕ (2𝑎) And 𝑘 = 𝑐 − 𝑏² ∕ (4𝑎) We Get.
It may be a surprise, but we don't need to evaluate any square root to do so! 𝑦 = 𝑎 (𝑥 − ℎ)² + 𝑘. The sign on a (plus or minus) tells you whether the quadratic's parabola opens up or opens down. Y = a ( x − h) 2 + k (h,k) is the vertex as you can see in the picture below if a is positive then the parabola opens upwards like a regular u.
Web When Written In Vertex Form :
(a will stay the same, h is x, and k is y). (𝑥 − ℎ)² ≥ 0 for all 𝑥. So the parabola will have a vertex when (𝑥 − ℎ)² = 0 ⇔ 𝑥 = ℎ ⇒ 𝑦 = 𝑘. In other words, for the vertex, (x, y) = (h, k).
Web When The Equation Is Reformatted As Above, The Point (H, K) Is The Vertex.
That is, both of the a 's have exactly the same value. While the standard quadratic form is a x 2 + b x + c = y, the vertex form of a quadratic equation is y = a ( x − h) 2 + k. 𝑎 < 0 ⇒ (ℎ, 𝑘) is the maximum point. • the h represents a horizontal shift (how far left, or right, the graph has shifted from x = 0).