Cartesian Form Vectors
Cartesian Form Vectors - (i) using the arbitrary form of vector →r = xˆi + yˆj + zˆk (ii) using the product of unit vectors let us consider a arbitrary vector and an equation of the line that is passing through the points →a and →b is →r = →a + λ(→b − →a) The vector form of the equation of a line is [math processing error] r → = a → + λ b →, and the cartesian form of the. Solution both vectors are in cartesian form and their lengths can be calculated using the formula we have and therefore two given vectors have the same length. Examples include finding the components of a vector between 2 points, magnitude of. Web this is 1 way of converting cartesian to polar. =( aa i)1/2 vector with a magnitude of unity is called a unit vector. The one in your question is another. The following video goes through each example to show you how you can express each force in cartesian vector form. We call x, y and z the components of along the ox, oy and oz axes respectively. First find two vectors in the plane:
The value of each component is equal to the cosine of the angle formed by. \hat i= (1,0) i^= (1,0) \hat j= (0,1) j ^ = (0,1) using vector addition and scalar multiplication, we can represent any vector as a combination of the unit vectors. The vector form of the equation of a line is [math processing error] r → = a → + λ b →, and the cartesian form of the. Web this formula, which expresses in terms of i, j, k, x, y and z, is called the cartesian representation of the vector in three dimensions. Show that the vectors and have the same magnitude. The following video goes through each example to show you how you can express each force in cartesian vector form. Examples include finding the components of a vector between 2 points, magnitude of. =( aa i)1/2 vector with a magnitude of unity is called a unit vector. In terms of coordinates, we can write them as i = (1, 0, 0), j = (0, 1, 0), and k = (0, 0, 1). I prefer the ( 1, − 2, − 2), ( 1, 1, 0) notation to the i, j, k notation.
Web learn to break forces into components in 3 dimensions and how to find the resultant of a force in cartesian form. In this unit we describe these unit vectors in two dimensions and in threedimensions, and show how they can be used in calculations. Find the cartesian equation of this line. Web any vector may be expressed in cartesian components, by using unit vectors in the directions ofthe coordinate axes. A b → = 1 i − 2 j − 2 k a c → = 1 i + 1 j. In terms of coordinates, we can write them as i = (1, 0, 0), j = (0, 1, 0), and k = (0, 0, 1). Examples include finding the components of a vector between 2 points, magnitude of. Web these vectors are the unit vectors in the positive x, y, and z direction, respectively. Web in cartesian coordinates, the length of the position vector of a point from the origin is equal to the square root of the sum of the square of the coordinates. First find two vectors in the plane:
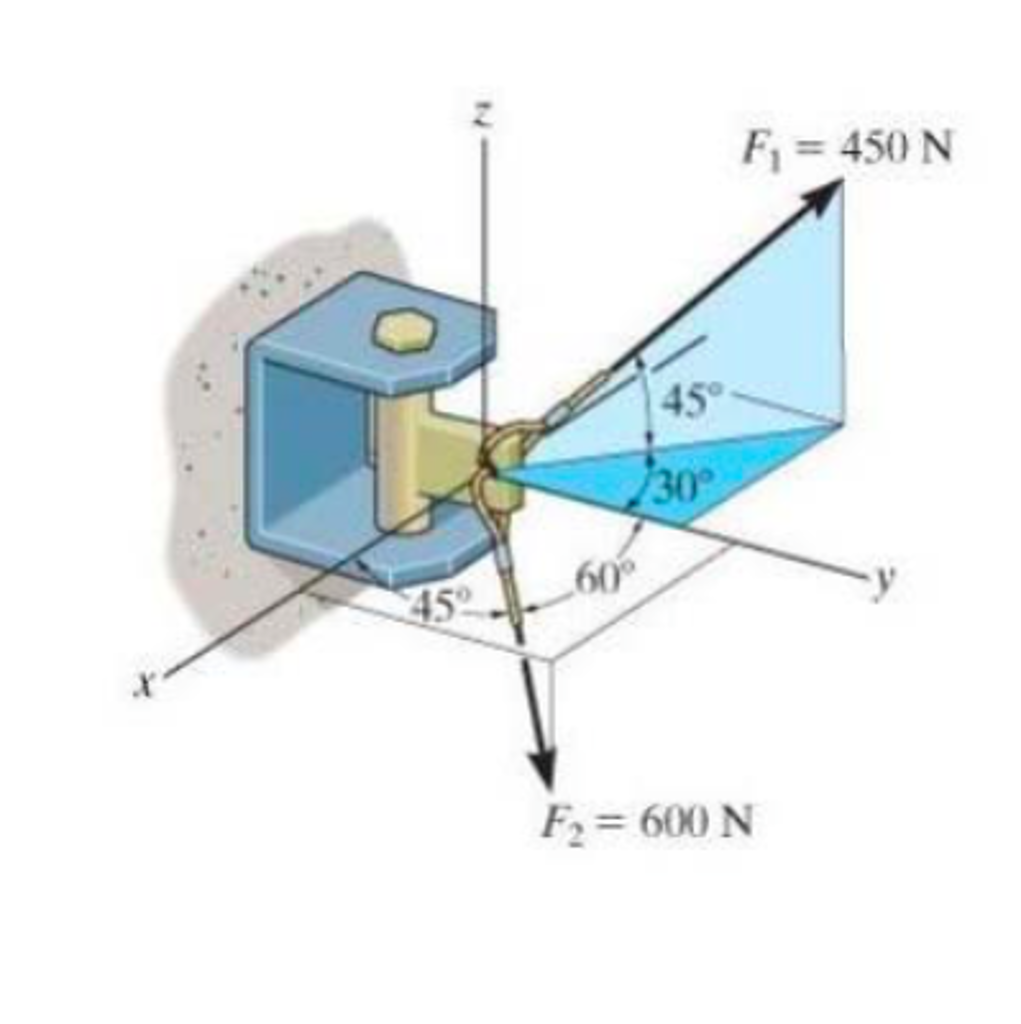
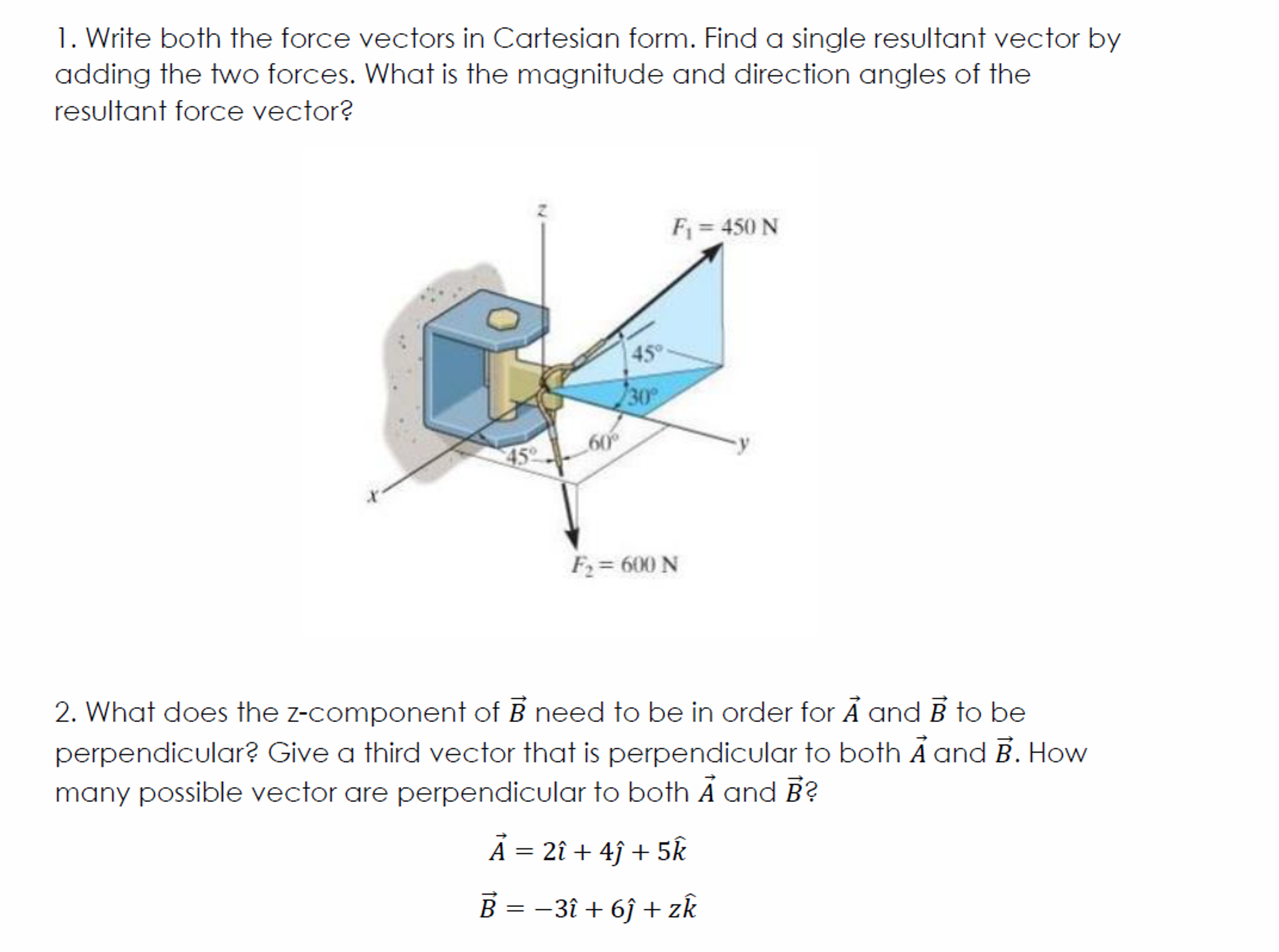
Solved 1. Write both the force vectors in Cartesian form.
Find the cartesian equation of this line. A b → = 1 i − 2 j − 2 k a c → = 1 i + 1 j. Here, a x, a y, and a z are the coefficients (magnitudes of the vector a along axes after. Web there are usually three ways a force is shown. The vector form.
PPT FORCE VECTORS, VECTOR OPERATIONS & ADDITION OF FORCES 2D & 3D
Examples include finding the components of a vector between 2 points, magnitude of. Web the cartesian form of representation of a point a(x, y, z), can be easily written in vector form as \(\vec a = x\hat i + y\hat j + z\hat k\). Web the components of a vector along orthogonal axes are called rectangular components or cartesian components..
Statics Lecture 2D Cartesian Vectors YouTube
The plane containing a, b, c. Web polar form and cartesian form of vector representation polar form of vector. Web when a unit vector in space is expressed in cartesian notation as a linear combination of i, j, k, its three scalar components can be referred to as direction cosines. So, in this section, we show how this is possible.
Engineering at Alberta Courses » Cartesian vector notation
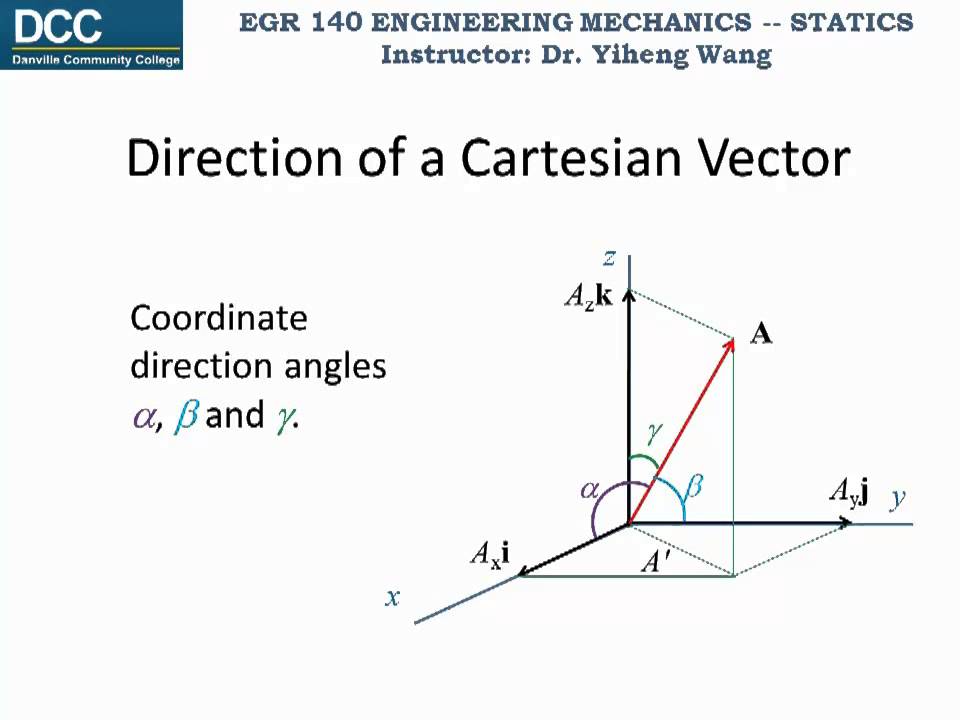
We talk about coordinate direction angles,. I prefer the ( 1, − 2, − 2), ( 1, 1, 0) notation to the i, j, k notation. The magnitude of a vector, a, is defined as follows. Observe the position vector in your question is same as the point given and the other 2 vectors are those which are perpendicular to.
Bab2
Applies in all octants, as x, y and z run through all possible real values. Web in cartesian coordinates, the length of the position vector of a point from the origin is equal to the square root of the sum of the square of the coordinates. The one in your question is another. For example, (3,4) (3,4) can be written.
Resultant Vector In Cartesian Form RESTULS
(i) using the arbitrary form of vector →r = xˆi + yˆj + zˆk (ii) using the product of unit vectors let us consider a arbitrary vector and an equation of the line that is passing through the points →a and →b is →r = →a + λ(→b − →a) Converting a tensor's components from one such basis to another.
Statics Lecture 05 Cartesian vectors and operations YouTube
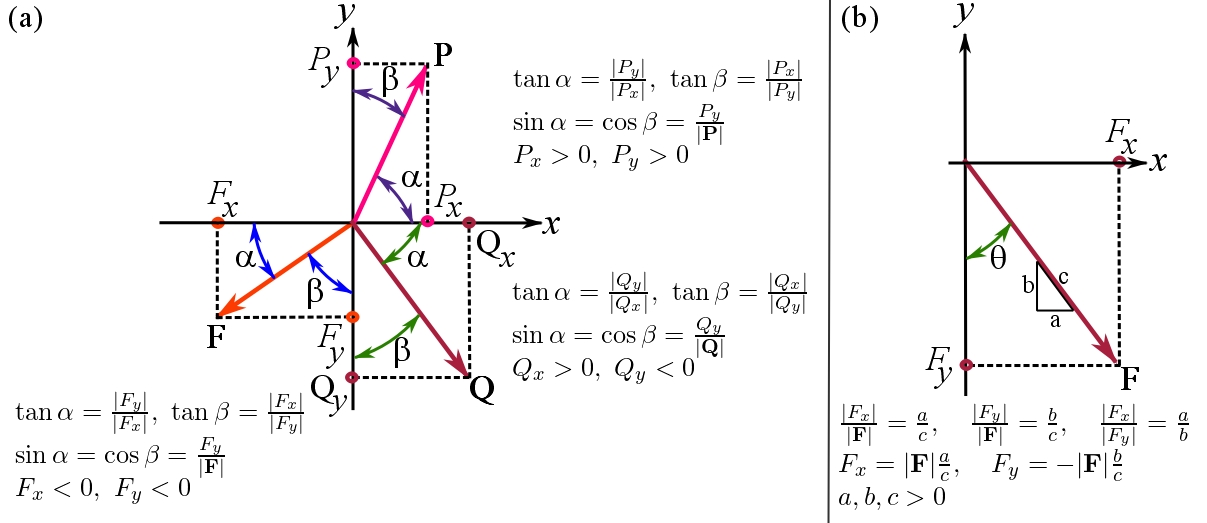
Magnitude & direction form of vectors. Web the vector form can be easily converted into cartesian form by 2 simple methods. Web any vector may be expressed in cartesian components, by using unit vectors in the directions ofthe coordinate axes. In this way, following the parallelogram rule for vector addition, each vector on a cartesian plane can be expressed as.
Solved Write both the force vectors in Cartesian form. Find
Web in cartesian coordinates, the length of the position vector of a point from the origin is equal to the square root of the sum of the square of the coordinates. Solution both vectors are in cartesian form and their lengths can be calculated using the formula we have and therefore two given vectors have the same length. =( aa.
Express each in Cartesian Vector form and find the resultant force
A vector decomposed (resolved) into its rectangular components can be expressed by using two possible notations namely the scalar notation (scalar components) and the cartesian vector notation. Magnitude & direction form of vectors. Web when a unit vector in space is expressed in cartesian notation as a linear combination of i, j, k, its three scalar components can be referred.
Introduction to Cartesian Vectors Part 2 YouTube
Applies in all octants, as x, y and z run through all possible real values. Web the vector form can be easily converted into cartesian form by 2 simple methods. The vector, a/|a|, is a unit vector with the direction of a. For example, (3,4) (3,4) can be written as 3\hat i+4\hat j 3i^+4j ^. Web when a unit vector.
Web Any Vector May Be Expressed In Cartesian Components, By Using Unit Vectors In The Directions Ofthe Coordinate Axes.
The following video goes through each example to show you how you can express each force in cartesian vector form. Web the vector form can be easily converted into cartesian form by 2 simple methods. So, in this section, we show how this is possible by defining unit vectorsin the directions of thexandyaxes. We talk about coordinate direction angles,.
=( Aa I)1/2 Vector With A Magnitude Of Unity Is Called A Unit Vector.
These are the unit vectors in their component form: Web the components of a vector along orthogonal axes are called rectangular components or cartesian components. The plane containing a, b, c. Web when a unit vector in space is expressed in cartesian notation as a linear combination of i, j, k, its three scalar components can be referred to as direction cosines.
In This Way, Following The Parallelogram Rule For Vector Addition, Each Vector On A Cartesian Plane Can Be Expressed As The Vector Sum Of Its Vector Components:
\hat i= (1,0) i^= (1,0) \hat j= (0,1) j ^ = (0,1) using vector addition and scalar multiplication, we can represent any vector as a combination of the unit vectors. Web polar form and cartesian form of vector representation polar form of vector. Web in cartesian coordinates, the length of the position vector of a point from the origin is equal to the square root of the sum of the square of the coordinates. Magnitude & direction form of vectors.
A Vector Decomposed (Resolved) Into Its Rectangular Components Can Be Expressed By Using Two Possible Notations Namely The Scalar Notation (Scalar Components) And The Cartesian Vector Notation.
Applies in all octants, as x, y and z run through all possible real values. In this unit we describe these unit vectors in two dimensions and in threedimensions, and show how they can be used in calculations. Examples include finding the components of a vector between 2 points, magnitude of. Web this is 1 way of converting cartesian to polar.