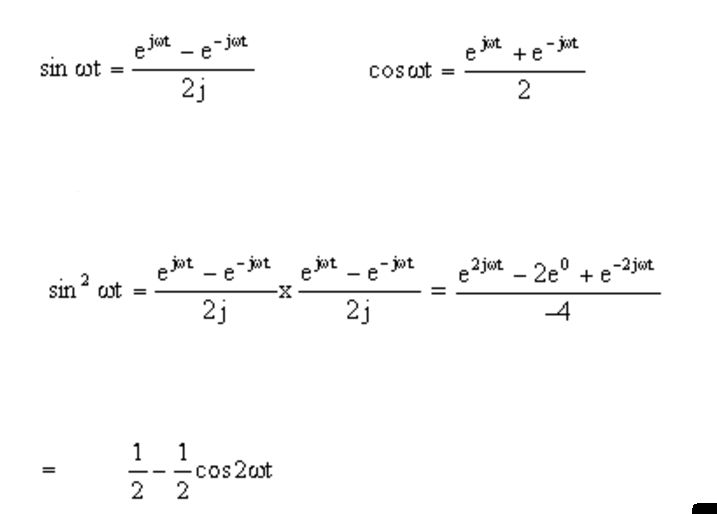
Cosine Exponential Form
Cosine Exponential Form - Here φ is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radians. Web $$e^{ix} = \cos x + i \sin x$$ fwiw, that formula is valid for complex $x$ as well as real $x$. Web relations between cosine, sine and exponential functions. This formula can be interpreted as saying that the function e is a unit complex number, i.e., it traces out the unit circle in the complex plane as φ ranges through the real numbers. Web now solve for the base b b which is the exponential form of the hyperbolic cosine: Web i am in the process of doing a physics problem with a differential equation that has the form: Y = acos(kx) + bsin(kx). Cos ( k ω t) = 1 2 e i k ω t + 1 2 e − i k ω t. Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and. Web the complex exponential form of cosine.
Y = acos(kx) + bsin(kx). After that, you can get. Web the second solution method makes use of the relation \(e^{it} = \cos t + i \sin t\) to convert the sine inhomogeneous term to an exponential function. Here φ is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radians. X = b = cosha = 2ea +e−a. Web now solve for the base b b which is the exponential form of the hyperbolic cosine: Web property of the exponential, now extended to any complex numbers c 1 = a 1+ib 1 and c 2 = a 2 + ib 2, giving ec 1+c 2 =ea 1+a 2ei(b 1+b 2) =ea 1+a 2(cos(b 1 + b 2) + isin(b 1 + b. Web 1 orthogonality of cosine, sine and complex exponentials the functions cosn form a complete orthogonal basis for piecewise c1 functions in 0 ˇ, z ˇ 0 cosm cosn d = ˇ 2 mn(1. Web i am in the process of doing a physics problem with a differential equation that has the form: Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and.
After that, you can get. Web the complex exponential form of cosine. Web i am in the process of doing a physics problem with a differential equation that has the form: X = b = cosha = 2ea +e−a. Web $$e^{ix} = \cos x + i \sin x$$ fwiw, that formula is valid for complex $x$ as well as real $x$. (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Web 1 orthogonality of cosine, sine and complex exponentials the functions cosn form a complete orthogonal basis for piecewise c1 functions in 0 ˇ, z ˇ 0 cosm cosn d = ˇ 2 mn(1. Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and. Y = acos(kx) + bsin(kx). Web the fourier series can be represented in different forms.
Solution One term of a Fourier series in cosine form is 10 cos 40πt
(45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. X = b = cosha = 2ea +e−a. Web the complex exponential form of cosine. Web 1 orthogonality of cosine, sine and complex exponentials the functions cosn form a complete orthogonal basis for piecewise c1 functions in 0 ˇ, z ˇ 0 cosm.
Exponential cosine fit A phase binned amplitude exemplar (Data) is
Web $$e^{ix} = \cos x + i \sin x$$ fwiw, that formula is valid for complex $x$ as well as real $x$. Web the complex exponential form of cosine. (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. X = b = cosha = 2ea +e−a. After that, you can get.
Basics of QPSK modulation and display of QPSK signals Electrical
X = b = cosha = 2ea +e−a. Web the fourier series can be represented in different forms. Web the complex exponential form of cosine. Web i am in the process of doing a physics problem with a differential equation that has the form: Web relations between cosine, sine and exponential functions.
EM to Optics 10 Converting Cos & Sine to Complex Exponentials YouTube
X = b = cosha = 2ea +e−a. Web $$e^{ix} = \cos x + i \sin x$$ fwiw, that formula is valid for complex $x$ as well as real $x$. This formula can be interpreted as saying that the function e is a unit complex number, i.e., it traces out the unit circle in the complex plane as φ ranges.
PPT Fourier Series PowerPoint Presentation ID390675
Web the complex exponential form of cosine. Cos ( k ω t) = 1 2 e i k ω t + 1 2 e − i k ω t. Web property of the exponential, now extended to any complex numbers c 1 = a 1+ib 1 and c 2 = a 2 + ib 2, giving ec 1+c 2 =ea.
Question Video Converting the Product of Complex Numbers in Polar Form
Y = acos(kx) + bsin(kx). After that, you can get. Here φ is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radians. Web 1 orthogonality of cosine, sine and complex exponentials the functions cosn form a complete orthogonal basis for piecewise c1 functions.
Complex Numbers 4/4 Cos and Sine to Complex Exponential YouTube
Web relations between cosine, sine and exponential functions. (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Web the complex exponential form of cosine. The trigonometric spectrum of cos ( k ω t) is single amplitude of the cosine function at a. Web now solve for the base b b which is.
Other Math Archive January 29, 2018
Cos ( k ω t) = 1 2 e i k ω t + 1 2 e − i k ω t. X = b = cosha = 2ea +e−a. The trigonometric spectrum of cos ( k ω t) is single amplitude of the cosine function at a. This formula can be interpreted as saying that the function e is.
Relationship between sine, cosine and exponential function
Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and. Cos ( k ω t) = 1 2 e i k ω t + 1 2 e − i k ω t. Web the fourier series can be represented in different forms. X = b =.
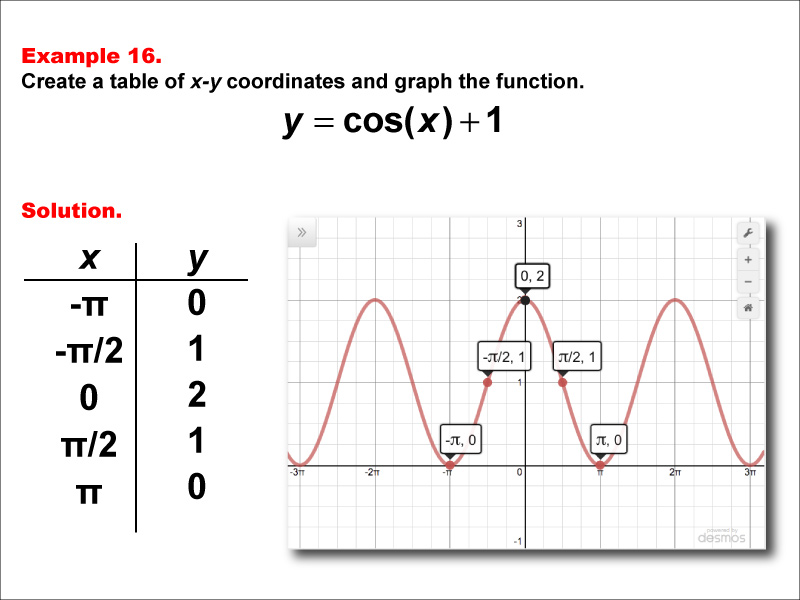
Math Example Cosine Functions in Tabular and Graph Form Example 16
X = b = cosha = 2ea +e−a. Web 1 orthogonality of cosine, sine and complex exponentials the functions cosn form a complete orthogonal basis for piecewise c1 functions in 0 ˇ, z ˇ 0 cosm cosn d = ˇ 2 mn(1. Cos ( k ω t) = 1 2 e i k ω t + 1 2 e −.
Web The Complex Exponential Form Of Cosine.
Here φ is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radians. Web i am in the process of doing a physics problem with a differential equation that has the form: X = b = cosha = 2ea +e−a. Web now solve for the base b b which is the exponential form of the hyperbolic cosine:
Web The Fourier Series Can Be Represented In Different Forms.
Cos ( k ω t) = 1 2 e i k ω t + 1 2 e − i k ω t. (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Y = acos(kx) + bsin(kx). Web relations between cosine, sine and exponential functions.
This Formula Can Be Interpreted As Saying That The Function E Is A Unit Complex Number, I.e., It Traces Out The Unit Circle In The Complex Plane As Φ Ranges Through The Real Numbers.
Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and. Web property of the exponential, now extended to any complex numbers c 1 = a 1+ib 1 and c 2 = a 2 + ib 2, giving ec 1+c 2 =ea 1+a 2ei(b 1+b 2) =ea 1+a 2(cos(b 1 + b 2) + isin(b 1 + b. Web 1 orthogonality of cosine, sine and complex exponentials the functions cosn form a complete orthogonal basis for piecewise c1 functions in 0 ˇ, z ˇ 0 cosm cosn d = ˇ 2 mn(1. The trigonometric spectrum of cos ( k ω t) is single amplitude of the cosine function at a.
Web $$E^{Ix} = \Cos X + I \Sin X$$ Fwiw, That Formula Is Valid For Complex $X$ As Well As Real $X$.
Web the second solution method makes use of the relation \(e^{it} = \cos t + i \sin t\) to convert the sine inhomogeneous term to an exponential function. After that, you can get.